Lehrgang nach dem aktuellen Fragenkatalog der Bundesnetzagentur. Zum Download des Fragenkatalogs

Hinweis: Für das sinnvolle Bearbeiten dieses Amateurfunklehrgangs benötigen Sie einen Taschenrechner, der außer den Grundfunktionen noch den Logarithmus (log) und die \(\frac{1}{x}\)-Funktion enthält.

Die Prüfung zum Amateurfunkzeugnis Klasse A enthält wesentlich mehr Berechnungen, als dies für Klasse E der Fall ist. Deshalb sollen hier die mathematischen Voraussetzungen zum besseren Verständnis der folgenden Kapitel geschaffen werden. Wenn Ihnen aber Mathematik "ein Gräuel" ist, beginnen Sie mit Kapitel 4 oder 5 und arbeiten Sie die ersten Kapitel später durch. Sie benötigen dazu die Formelsammlung aus dem Fragenkatalog.

Größen und Einheiten

Bereits im Lehrgang zur Klasse E haben Sie das SI-Einheiten-System (System International) kennen gelernt. In dem System sind sieben Basisgrößen (Länge, Masse, Zeit, Stromstärke, Temperatur, Stoffmenge, Lichtstärke) und die zugehörigen Basiseinheiten festgelegt. Hier noch einmal die übersicht:

Basisgrößen	Einheiten	Zeichen
Länge	Meter	m
Masse	Kilogramm	kg
Zeit	Sekunde	s
Stromstärke	Ampere	A
Temperatur	Kelvin	K
Stoffmenge	Mol	mol
Lichtstärke	Candela	cd

Man nennt dieses System in der Reihenfolge der Einheiten auch MKSA-KMC-System oder kurz MKSA-System, weil die vier ersten Einheiten die wichtigsten sind. Alle anderen Einheiten können hieraus abgeleitet werden.

Testen Sie sich, indem Sie links auf die Fragezeichen klicken, aber nur einmal in jeder Tabelle!

ehemalige Prüfungsfrage

TA106  Welche der nachfolgenden Antworten enthält nur Basiseinheiten nach dem internationalen Einheitensystem?
	Meter, Kelvin, Sekunde, Ampere
	Radiant, Meter, Volt, Watt
	Farad, Henry, Ohm, Sekunde
	Grad, Hertz, Ohm, Sekunde

Sie haben die Frage gut beantwortet, wenn Sie in der linken Spalte nur einmal das Wort "Richtig" sehen und keinmal "Falsch".

Aus diesen Basiseinheiten ergeben sich alle abgeleiteten gesetzlichen Einheiten, wie zum Beispiel Fläche, Dichte, Frequenz, Energie, Leistung, Spannung, Widerstand und so weiter.

Abgeleitete Einheiten

Größe	Formel­buchstabe	Maßeinheit	Abk. der Einheit
Ladung	Q	Coulomb	C = As
Spannung	U	Volt	V
Leistung	P	Watt	W = V · A
Arbeit	W	Wattsekunde	Ws = VAs
El. Feldstärke	E	Volt pro Meter	V/m
Magn. Feldstärke	H	Ampere pro Meter	A/m
Flussdichte	B	Tesla	Vs/m2
Frequenz	f	Hertz	Hz=1/s
Widerstand, Impedanz	R	Ohm	Ω=V/A
Leitwert	G	Siemens	S=1/Ω
Kapazität	C	Farad	F=As/V
Induktivität	L	Henry	H=Vs/A

ehemalige Prüfungsfrage

TA101  Welche Einheit wird für die elektrische Feldstärke verwendet?
	Henry pro Meter (H/m)
	Watt pro Quadratmeter (W/m2)
	Ampere pro Meter (A/m)
	Volt pro Meter (V/m)

ehemalige Prüfungsfrage

TA102  Welche Einheit wird für die magnetische Feldstärke verwendet?
	Amperemeter (Am)
	Tesla (T)
	Ampere pro Meter (A/m)
	Henry pro Meter (H/m)

ehemalige Prüfungsfrage

TA103  In welcher Einheit wird die Impedanz angegeben?
	Siemens
	Farad
	Ohm
	Henry

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TA104  Die Einheit "Siemens" wird verwendet für die Angabe
	der Impedanz einer Leitung.
	des ohmschen Widerstands.
	des Leitwertes eines Widerstands.
	der magnetischen Feldstärke.

ehemalige Prüfungsfrage

TA105  Wenn [s] für Sekunde steht, gilt für die Einheit der Frequenz
	\( \large \text{Hz} = \frac{1}{s} \)
	\( \large \text{Hz} = s \)
	\( \large \text{Hz} = s^2 \)
	\( \large \text{Hz} = \frac{1}{s^2} \)

Lösungsweg (hier klicken zum Anzeigen):

Zehnerpotenzen

Das Messergebnis kann ein Vielfaches oder ein Teil einer Einheit sein. Es werden meist dezimale Vielfache oder Teile von Einheiten benutzt, zum Beispiel kilo für tausendfach oder milli für ein Tausendstel. Auch die folgende Tabelle ist aus dem Lehrgang zur Klasse E bekannt.

Faktor	Potenz	Vorsatz
billionenfach	1012	Tera	T
milliardenfach	109	Giga	G
millionenfach	106	Mega	M
tausendfach	103	kilo	k
hundertfach	102	hekto	h
zehnfach	101	deka	da
zehntel	10-1	dezi	d
hundertstel	10-2	zenti	c
tausendstel	10-3	milli	m
millionstel	10-6	mikro	µ
milliardstel	10-9	nano	n
billionstel	10-12	piko	p

Achten Sie darauf, dass die Abkürzungen für Tera, Giga und Mega mit großen Buchstaben und alle anderen mit kleinen Buchstaben geschrieben werden. Besonders wichtig ist es bei m oder M (milli oder Mega) und bei k für kilo, denn das große K wird in der Digitaltechnik auch für Kilo verwendet, wobei dort K = 1024 ist. 1 Kilobyte (1 KB) sind 1024 Byte.

1 · 10^-6 ist gleichbedeutend mit \[ \frac{1}{10^{+6}} = \frac{1}{1000000} = 0{,}000001 \] Für die Umwandlung in kilo, milli, mikro und so weiter ist es zweckmäßig, wenn die Hochzahlen die Werte 3 (kilo), 6 (Mega), 9 (Giga) oder -3 (milli), -6 (mikro), -9 (nano) oder -12 (piko) haben.

ehemalige Prüfungsfrage

TA111  100 mW entspricht
	0,01 W.
	0,001 W.
	10-1W.
	10-2W.

Lösungsweg (hier klicken zum Anzeigen):

Prozent, Promille, „ppm“

Übersicht

Wert	als Teiler	als Bruch	als Zehnerpotenz
1 Prozent	1 Hundertstel	1/100	10-2
1 Promille	1 Tausendstel	1/1000	10-3
1 ppm	1 Millionstel	1/1000000	10-6

Prozent ist 1/100 oder 10^-2. Man braucht also nur das Komma um zwei Stellen, bei Promille um drei Stellen nach links zu verschieben.

Beispiel
1 % von 14300 kHz sind 143 kHz.
2 % von 14300 kHz sind 2 mal 143 kHz, also 286 kHz.
1 Promille von 14300 kHz sind 14,3 kHz.

ppm kommt von parts per million (Teile von einer Million). Diese Angabe wird bei der Genauigkeit von Frequenzen, bei der Frequenzstabilität von Transceivern oder Temperaturstabilität von Quarzen und so weiter verwendet.

ehemalige Prüfungsfrage

TA118  Die digitale Anzeige eines Senders hat eine Anzeigegenauigkeit von 10 ppm. Sie zeigt die Sendefrequenz von 14,25 MHz an. In welchen Grenzen kann sich die tatsächliche Frequenz bewegen?
	Zwischen 14,24998575  und       14,25001425 MHz
	Zwischen 14,2498575    und       14,2501425 MHz
	Zwischen 14,249998575 und      14,250001425 MHz
	Zwischen 14,248575      und       14,251425 MHz

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TA117  Eine Genauigkeit von 1 ppm entspricht
	0,0001 %
	0,001 %
	0,01 %
	0,1 %

Lösungsweg (hier klicken zum Anzeigen):

Formeln umstellen

Im Fragenkatalog gibt es unter Punkt 1.1.1 Allgemeine mathematische Kenntnisse einen Hinweis, dass der erforderliche Prüfungsstoff in den folgenden Abschnitten enthalten ist. Weil das Umstellen von Formeln praktisch Grundvoraussetzung für die Lösung aller Aufgaben ist, soll es in einem kleinen Vorspann geübt werden. Die mit ÜB gekennzeichneten Aufgaben gibt es im Fragenkatalog nicht. Sie dienen als Vorübung. Recht häufig kommt die einfache Formelumstellung vor, bei der das Ohmsche Gesetz \[ U = R \cdot I \] oder die einfache Leistungsformel \[ P = U \cdot I \] nach einer der drei Größen umgestellt werden muss. Mathematisch funktioniert es so, dass man einfach auf beiden Seiten durch diejenige Größe teilt, die man weg haben möchte.
Beispiel \[ P = U \cdot I \] soll nach I umgestellt werden.
Lösung: Man dividiert auf beiden Seiten der Gleichung durch U und I bleibt auf einer Seite übrig.

Wie Sie bereits im Lehrgang zur Klasse E gelernt haben, kann folgendes Hilfsmittel benutzt werden. Man schreibt die Formel in folgender Weise in ein Dreieck.

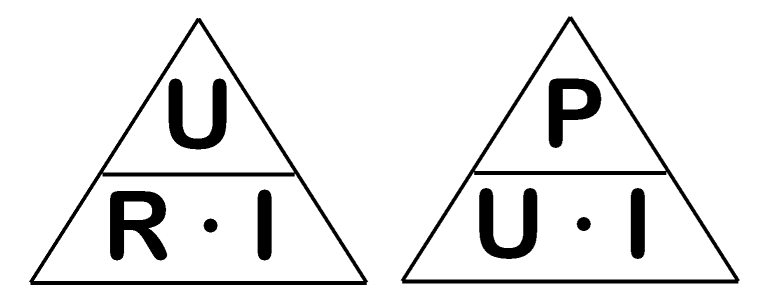
Die Anwendung dieses Dreiecks funktioniert folgendermaßen. Wenn man beispielsweise beim Ohmschen Gesetz nach dem Strom umstellen will, hält man den Buchstaben I zu und schaut, was übrig bleibt. Der waagerechte Strich ersetzt den Bruchstrich. Also in diesem Fall ist \[ I = \frac{U}{R} \]

In der Prüfung kommen recht schwierige Formelumstellungen vor, die am Beispiel der Leistungsformel mit dem Widerstand geübt werden sollen. Wenn Sie allerdings zu solchen mathematischen Exkursionen keine Lust haben, können Sie versuchen, sich die Antworten zu merken und mit dem nächsten Abschnitt Dezibel weiter machen.

ehemalige Prüfungsfrage

TB923  In welcher Antwort sind alle dargestellten Zusammenhänge zwischen Strom, Spannung, Widerstand und Leistung richtig?
	\( \large I = \sqrt{\frac{P}{R}} ; \ \ U = \sqrt{P \cdot R} \)
	\( \large I = \sqrt{P \cdot R} ; \ \ U = \sqrt{\frac{P}{R}} \)
	\( \large I = \sqrt{\frac{R}{P}} ; \ \ U = \sqrt{P \cdot R} \)
	\( \large I = \frac{\sqrt{P}}{R} ; \ \ U = \sqrt{P} \cdot R \)

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TB924  In welcher Antwort (Zeile) sind alle dargestellten Zusammenhänge zwischen Widerstand, Leistung, Spannung und Strom richtig?
	\( \large R = \frac{U^2}{P} ; \ \ R = \frac{P}{I^2} \)
	\( \large R = U^2 \cdot P; \ \ R = \frac{P}{I^2} \)
	\( \large R = \frac{P}{U^2}; \ \ R = P \cdot I^2 \)
	\( \large R = \frac{U^2}{P}; \ \ R = P \cdot I^2 \)

Lösungsweg (hier klicken zum Anzeigen):

Übungsfrage

ÜB101  Stellen Sie die Formel um nach der Größe R: \( \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} \) Welche Lösung ist richtig?
	\( \large R = \frac{R_1 + R_2}{R_1 \cdot R_2} \)
	\( \large R = \frac{R_1 \cdot R_2}{R_1 + R_2} \)
	\( \large R = \frac{R_1 \cdot R_2}{R_1 - R_2} \)
	\( \large R = \frac{R_1 - R_2}{R_1 \cdot R_2} \)

Lösungsweg (hier klicken zum Anzeigen):

Übungsfrage

ÜB102  Stellen Sie die Formel um nach der Größe R1. \( R = \frac{R_1 \cdot R_2}{ R_1 + R_2} \) Welche Lösung ist richtig?
	\( \large R_1 = \frac{R_2 \cdot R}{R_2 - R} \)
	\( \large R_1 = \frac{R_2 - R}{R_2 \cdot R} \)
	\( \large R_1 = \frac{R \cdot R_2}{R - R_2} \)
	\( \large R_1 = \frac{R_2 \cdot R}{R_2 + R} \)

Lösungsweg (hier klicken zum Anzeigen):

Das Dezibel

Im Amateurfunklehrgang für die Klasse E wurde im Bereich E10 dem Dezibel fast ein komplettes Kapitel gewidmet. Hier folgt eine kleine Zusammenfassung in Form der Leistungsformel.

Wenn Leistungen gegeben sind, rechnet man bei einem Verstärker

\[ v = 10 \cdot \lg \frac{P_2}{P_1}[\text{dB}] \]

P₁ = Eingangsleistung, P₂ = Ausgangsleistung

Übungsfrage

ÜB103  Wie viel Dezibel (dB) entsprechen einer vierfachen Leistung?
	3 dB
	6 dB
	10 dB
	16 dB

Lösungsweg (hier klicken zum Anzeigen):

Merken Sie sich: 4-facher Leistung entsprechen 6 dB

Rechnen Sie außerdem einmal mit dem Faktor 2 (2 Watt und 1 Watt) und mit dem Faktor 10 (10 Watt und 1 Watt) und merken Sie sich diese Werte ebenfalls. Sie finden die Ergebnisse in folgender Tabelle.

Leistungsfaktor	Dezibel
2	3 dB
4	6 dB
10	10 dB

ehemalige Prüfungsfrage

TD417  Ein Leistungsverstärker hebt die Eingangsleistung von 2,5 Watt auf 38 Watt Ausgangsleistung an. Wie groß ist die Leistungsverstärkung in dB?
	11,8 dB
	15,2 dB
	17,7 dB
	23,6 dB

Lösungsweg (hier klicken zum Anzeigen):

Praktisch bei der Rechnung mit Dezibel ist, dass man diese Werte einfach addieren kann, wenn mehrere Verstärkungen oder Gewinne gegeben sind und subtrahieren, wenn beispielsweise bei Kabeln Dämpfungen auftreten.

Beispiel

Dezibel	10 dB	+	3 dB	=	13 dB
Leistungs- faktoren	10	·	2	=	20

Rechnen Sie nach! Machen Sie die Probe, indem Sie Logarithmus von 20 und dann mal 10 rechnen! Es muss 13 dB heraus kommen.
Haben Sie beispielsweise einen Sender mit 1 Watt Ausgangsleistung, dahinter eine Endstufe mit 10 dB Leistungsverstärkung und daran angeschlossen eine Antenne mit 3 dB Gewinn (Gewinn verhält sich wie Verstärkung), dann haben Sie einen Leistungsfaktor von 20 und damit 20 Watt Strahlungsleistung. Diese Strahlungsleistung nennt man auch ERP (effective radiated power). Mehr dazu unter Antennentechnik!

Umgekehrt wird es schwieriger, nämlich aus einem gegebenen dB-Wert den Verstärkungsfaktor zu berechnen.

ehemalige Prüfungsfrage

TD418  Ein HF-Verstärker hat einen Gewinn von 16 dB. Welche Leistung ist am HF-Ausgang bei einer Eingangsleistung von 1 W?
	1 W
	4 W
	16 W
	40 W

Lösungsweg (hier klicken zum Anzeigen):

Man kann Dämpfungen und Verstärkungen (Gewinne) sehr einfach miteinander verrechnen.

Beispiel:

ÜB103   Sie haben einen Sender mit 10 Watt Ausgangsleistung, dahinter ein Antennenkabel mit 2 dB Dämpfung und daran angeschlossen eine Antenne mit 8 dB Gewinn (gegenüber dem Dipol). Wie groß ist die ERP?

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TA108  Einer Leistungsverstärkung von 40 entsprechen
	60 dB
	32 dB
	24 dB
	16 dB

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TB920  Eine HF-Ausgangsleistung von 100 W wird in eine angepasste übertragungsleitung eingespeist. Am antennenseitigen Ende der Leitung beträgt die Leistung 50 W bei einem Stehwellenverhältnis von 1,0. Wie hoch ist die Leitungsdämpfung?
	3 dB
	-3 dB
	6 dB
	-6 dB

Lösungsweg (hier klicken zum Anzeigen):

Merken Sie sich: Bei Dämpfungen rechnen Sie Eingangsleistung zu Ausgangsleistung und
bei Verstärkungen rechnen Sie Ausgangsleistung zu Eingangsleistung.

Dezibel bei Spannungen

Wenn Spannungen an einem bestimmten Widerstand gegeben sind, kann man für Leistung \( P = \frac{U^2}{R} \) einsetzen und erhält \[ a = 10 \cdot \lg \frac{U_1^2 \cdot R}{R \cdot U_2^2} [\text{dB}] \] R kann man kürzen und die Quadrate zusammenfassen. \[ a = 10 \cdot \lg \left(\frac{U_1}{U_2} \right)^2 [\text{dB}] \] und schließlich nach dem Logarithmengesetz \( \lg (b^x) = x \cdot \lg(b) \) wird daraus \[ a_U = 20 \cdot \lg\frac{U_1}{U_2}[\text{dB}] \] U₁ = Eingangsspannung, U₂ = Ausgangsspannung

ehemalige Prüfungsfrage

TA107  Einem Spannungsverhältnis von 15 entsprechen
	52 dB
	47 dB
	23,5 dB
	11,7 dB

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TD416  Ein NF-Verstärker hebt die Eingangsspannung von 1 mV auf 4 mV Ausgangsspannung an. Eingangs- und Ausgangswiderstand sind gleich. Wie groß ist die Spannungsverstärkung?
	3 dB
	6 dB
	9 dB
	12 dB

Lösungsweg (hier klicken zum Anzeigen):

Der Leistungspegel

In der Sendertechnik gibt man häufig die Ausgangsleistung nicht in Watt an, sondern in einem Verhältnis in Dezibel bezogen entweder auf ein Milliwatt oder ein Watt. Dies hat den Vorteil, dass man sofort Gewinnangaben von Antennen oder Verluste von Kabeln in Dezibel damit verrechnen kann.

Der Pegel dBm

\[ p = 10 \cdot \lg \left( \frac{P}{1 \ \text{mW}} \right) [\text{dBm}] \]

dBm steht für Dezibel bezogen auf ein Milliwatt.

Übungsfrage

ÜB104  Ein Sender hat eine Ausgangsleistung von 5 Watt. Angeschlossen ist ein Kabel mit insgesamt 2 dB Dämpfung und eine Antenne mit 10 dB Gewinn. Wie groß ist der Ausgangspegel in dBm?

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TA112  Ein Sender mit 1 Watt Ausgangsleistung ist an eine Endstufe mit einer Verstärkung von 10 dB angeschlossen. Wie groß ist der Ausgangspegel der Endstufe?
	10 dBm
	20 dBm
	30 dBm
	40 dBm

Lösungsweg (hier klicken zum Anzeigen):

Der Pegel dBW

\[ \boxed{p = 10 \cdot \lg \left( \frac{P}{1 \ \text{W}} \right) [\text{dBW}]} \]

Hierbei ist der Bezugswert 1 Watt.

ehemalige Prüfungsfrage

TA113  Der Ausgangspegel eines Senders beträgt 20 dBW. Dies entspricht einer Ausgangsleistung von
	100,5W
	101W
	102W
	1020W

Lösungsweg (hier klicken zum Anzeigen):

Der Spannungspegel

Dort, wo nur Spannungen auftreten und keine Leistungen, kann man auch einen Spannungspegel definieren, zum Beispiel bei der elektrischen Feldstärke, die in Volt pro Meter angegeben wird. Ein häufig gebrauchter Bezugswert ist 1 Mikrovolt. Dann lautet die Formel für den Spannungspegel

\[ p = 20 \cdot \lg \left( \frac{U}{1 \ \text{µV}} \right) [\text{dBµV}] \]

Beispiel
Welchen Spannungspegel in dBµV ergibt die Spannung 1 Volt?

Lösung mit der Formel \[ \begin{align} p &= 20 \cdot \lg \left( \frac{1 \ \text{V}}{1 \ \text{µV}} \right) [\text{dBµV}] \\ \\ p &= 20 \cdot \lg \left( 10^6 \right) [\text{dBµV}] \\ \\ p &= 20 \cdot 6 \text{dBµV} = \mathbf{120 \ \text{dBµV}} \end{align} \] Damit lösen Sie umgekehrt leicht folgende Prüfungsfrage.

ehemalige Prüfungsfrage

TA110  Der Pegelwert 120 dBµV/m entspricht einer elektrischen Feldstärke
	1 V/m.
	10 V/m.
	1000 V/m.
	1000 kV/m.

Lösung: Siehe Beispiel oberhalb!

Die S-Stufen

Eine weitere Anwendung der dB-Rechnung sind die „S-Stufen“ im Amateurfunk. In der Empfangstechnik hat man für die Angabe der Empfangsfeldstärke im RST-System für die Lautstärke S9 einen bestimmten Eingangspegel festgelegt. Mehr dazu im Lehrgang zu Klasse E!

Zusammenfassung aus dem Lehrgang Klasse E:

Kurzwelle: S9 entspricht 50µV an 50 Ω
UKW:          S9 entspricht 5 µV an 50 Ω

Jede S-Stufe entspricht 6 dB. 6 dB entsprechen einem Faktor 2 bei Spannungen, S8 hat also bei Kurzwelle einen Wert von 25 µV. Tabelle der S-Werte in µV:

	S9	S8	S7	S6	S5	S4	S3	S2	S1
KW	50	25	12,5	6,25	3,12	1,56	0,78	0,39	0,2
UKW	5	2,5	1,25	0,62	0,31	0,16	0,80	0,04	0,02

Bei Kurzwelle zum Beispiel entspricht S1 einer Empfangsspannung von 0,2 µV (das ist kleiner als Grenzempfindlichkeit) und bei UKW entspricht S1 = 20 nV (Nanovolt). Welcher Empfänger macht daraus ein lesbares Signal? S0 gibt es nicht.

Um auch Empfangsspannungen größer als 50 µV (bzw. 5 µV bei UKW) im RST-System angeben zu können, nennt man einfach die Dezibel über S9 als Zahlenwerte.

Übungsfrage

ÜB105  Welcher Empfangsspannung entspricht die Angabe S9+40 dB auf Kurzwelle?

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TA109  Wie groß ist der Unterschied von S4 nach S7 in dB?
	3 dB
	9 dB
	18 dB
	28 dB

Lösung: 3 S-Stufen entsprechen 3 mal 6 dB = 18 dB

Viel Erfolg beim Lehrgang wünscht Ihnen Eckart Moltrecht DJ4UF!

Nach Oben

Zur Lehrgangs-Übersicht Technik Klasse A

Copyright-Hinweis:
	Dieser DARC-Online-Lehrgang wurde mit freundlicher Genehmigung des Autors Eckart K. W. Moltrecht aus seinen Büchern "Amateurfunk-Lehrgang für das Amateurfunkzeugnis" aus dem VTH-Verlag (möglicherweise einer älteren Auflage!) für das Internet umgewandelt. Das Copyright liegt beim Autor und beim Verlag. Mehr über den Autor!
	Die Darstellung auch nur von Auszügen oder Zeichnungen oder Fotos im Internet ist untersagt. Für die private Verwendung können Sie gern eine Genehmigung beim Autor erhalten. Schreiben Sie eine E-Mail an eckart.moltrecht(at)gmail.com!

Letzte Bearbeitung: 10.06.2017 DJ4UF, 04.04.2020 DH8GHH
Fehlermeldungen mit Linkangabe an DH8GHH@darc.de