DARC-Online-Lehrgang Technik Klasse A Kapitel 2: Der Widerstand und seine Grundschaltungen
Neue Ausbildungsplattform 50ohm.de
Das Ausbildungsmaterial für den neuen Fragenkatalog (2024) findest du auf www.50Ohm.de
Hinweis: Der Lehrgang auf dieser Seite bezieht sich auf die alten Fragenkataloge, nach denen nur noch bis April 2024 geprüft wurde.
Kapitel 2: Der Widerstand und seine Grundschaltungen
In diesem Kapitel werden Prüfungsaufgaben aus folgenden Gebieten vorgestellt und ausführlich besprochen. Die Theorie dazu müsste aus dem Lehrgang für Klasse E bekannt sein. Jedoch werden für Klasse A mehr Berechnungen verlangt.
Inhaltsübersicht
- Leitfähigkeit
- Leiterwiderstand
- Ohmsches Gesetz
- Widerstand
- Innenwiderstand
- Leistung, Belastbarkeit
- Reihen- und Parallelschaltung
- Gemischte Schaltung von Widerständen
Die elektrische Leitfähigkeit
Verschiedene Materialien leiten den Strom unterschiedlich gut. Zur Leitfähigkeit finden Sie im Lehrgang zur Klasse E im Kapitel 4 einen Abschnitt Spezifischer Widerstand - Spezifischer Leitwert mit folgender Tabelle.
| Werkstoff | Spezifischer Leitwert | Einheit |
| Silber | 63 | \[ \frac{\text{A} \cdot \text{m}}{\text{V} \cdot \text{mm}^2} \] oder \[ \frac{\text{m}}{\Omega \cdot \text{mm}^2} \] |
| Kupfer | 56 | |
| Gold | 45 | |
| Aluminium | 37 | |
| Eisen | 10 | |
| Zinn | 8 | |
| Blei | 5 |
Aus Tabelle 4-1 Klasse E: Leitfähigkeit
ehemalige Prüfungsfrage
| TB106 Was verstehen Sie unter Halbleitermaterialien? | |
|---|---|
| Einige Stoffe (z.B. Silizium, Germanium) sind in reinem Zustand bei Zimmertemperatur gute Leiter. Durch geringfügige Zusätze von geeigneten anderen Stoffen nimmt jedoch ihre Leitfähigkeit ab. | |
| Einige Stoffe wie z.B. Indium oder Magnesium sind in reinem Zustand bei Zimmertemperatur gute Isolatoren. Durch geringfügige Zusätze von Silizium, Germanium oder geeigneten anderen Stoffen werden sie jedoch zu Leitern. | |
| Einige Stoffe (z.B. Silizium, Germanium) sind in reinem Zustand bei Zimmertemperatur gute Isolatoren. Durch geringfügige Zusätze von geeigneten anderen Stoffen oder bei hohen Temperaturen werden sie jedoch zu Leitern. | |
| Einige Stoffe (z.B. Silizium, Germanium) sind in trockenem Zustand bei Zimmertemperatur gute Elektrolyten. Durch geringfügige Zusätze von Wismut oder Tellur kann man daraus entweder N-leitendes- oder P-leitendes Material für Anoden bzw. Katoden von Halbleiterbauelementen herstellen. | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB105 Welche Gruppe von Materialien enthält nur Nichtleiter? | |
|---|---|
| Epoxyd, Polyethylen (PE), Polystyrol (PS) | |
| Pertinax, Polyvinylchlorid (PVC), Graphit | |
| Polyethylen (PE), Messing, Konstantan | |
| Teflon, Pertinax, Bronze | |
Lösungsweg (hier klicken zum Anzeigen):
Der Leiterwiderstand
ehemalige Prüfungsfrage
| TB104 Der Temperaturkoeffizient für den Widerstand von metallischen Leitern ist | |
|---|---|
| exponentiell | |
| negativ | |
| logarithmisch | |
| positiv | |
Lösungsweg (hier klicken zum Anzeigen):
Mit Hilfe des spezifischen Widerstandes kann man den Widerstand eines Leiters berechnen. Folgende Formel finden Sie im Anhang (Formelsammlung der BNetzA). \[ R = \frac{\rho \cdot l}{A} \] Der spezifische Widerstand ρ (rho) ist der Kehrwert des spezifischen Leitwerts und wird angegeben als der Widerstand in Ohm bei 1 m Länge und 1 mm2 Querschnitt.
ehemalige Prüfungsfrage
| TB101 Der spezifische Widerstand eines Drahtes (Leiters) ist definiert als der Widerstand | |
|---|---|
| bei einer Länge von 1 m und einem Querschnitt von 0,1 mm2. | |
| bei einer Länge von 100 mm und einem Querschnitt von 1 mm2. | |
| bei einer Länge von 1000 mm und einem Querschnitt von 1 mm2. | |
| bei einer Länge von 100 mm und einem Querschnitt von 0,1 mm2. | |
Lösungsweg (hier klicken zum Anzeigen):
Bei der folgenden Prüfungsfrage ist Mathematik gefragt. Sie brauchen außer der Formel für den Widerstand auch noch die Formel zur Berechnung der Querschnittsfläche eines kreisförmigen Leiters. Wenn Ihnen diese Mathematik nicht liegt, müssen Sie sich das sehr einfache Ergebnis merken, denn die Prüfungsfrage wird immer mit diesen Werten gestellt.
ehemalige Prüfungsfrage
| TB102 Welchen Widerstand hat eine Kupferdrahtwicklung, wenn der verwendete Draht eine Länge von 1,8 m und einen Durchmesser von 0,2 mm hat | |
|---|---|
| 0,05 Ω | |
| 1 Ω | |
| 5,6 Ω | |
| 56 Ω | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB103 Zwischen den Enden eines Kupferkabels mit einem Querschnitt von 0,5 mm2 messen Sie einen Widerstand von 1,5 Ohm. Wie lang ist das Kabel? | |
|---|---|
| 4,2 m | |
| 25,3 m | |
| 42,1 m | |
| 168,5 m | |
Lösungsweg (hier klicken zum Anzeigen):
Der Skin-Effekt
Jeder stromdurchflossene Leiter erzeugt ein Magnetfeld. Dieses Magnetfeld verläuft auch im Innern eines Kupferleiters. Durch das Magnetfeld werden besonders bei hohen Frequenzen die Elektronen aus der Mitte des Leiters zusammengedrängt. Es wirkt sich so aus, als ob die Querschnittsfläche für den Stromfluss geringer wird. Bei Frequenzen ab zirka 10 MHz wirkt sich dieser Effekt so stark aus, dass die Elektronen praktisch nur noch an der Oberfläche (englisch: skin) des Leiters fließen.
Um die Leitfähigkeit zu verbessern, versilbert man die Oberfläche des Leiters. Oder man stellt den Leiter für Hochfrequenz aus vielen voneinander isolierten dünnen Drähten her, die in mehreren Stufen miteinander verdrillt werden. Besonders für Antennendrähte und für Hochfrequenzspulen werden solche Drähte verwendet.
ehemalige Prüfungsfrage
| TC314 Welche Folgen hat der Skin-Effekt? | |
|---|---|
| Der Skin-Effekt ist für den mit der Frequenz ansteigenden induktiven Widerstand verantwortlich | |
| Der Strom fließt bei hohen Frequenzen nur noch in der Oberfläche des Leiters. Mit sinkendem stromdurchflossenen Querschnitt steigt daher der induktive Widerstand des Leiters. | |
| Der Strom fließt bei hohen Frequenzen nur noch in der Oberfläche des Leiters. Mit sinkendem stromdurchflossenen Querschnitt vergrößert sich daher der kapazitive Widerstand des Leiters | |
| Der Strom fließt bei hohen Frequenzen nur noch in der Oberfläche des Leiters. Mit sinkendem stromdurchflossenen Querschnitt steigt daher der effektive Widerstand des Leiters | |
ehemalige Prüfungsfrage
| TC315 Was verstehen Sie unter dem technischen Ausdruck Skin-Effekt? | |
|---|---|
| Als Skin-Effekt bezeichnet man die Erscheinung, dass sich mit steigender Frequenz der Elektronenstrom mehr und mehr zu den Kanten eines Kondensators hin verlagert. Dadurch erhöht sich mit steigender Frequenz die Kapazitä | |
| Als Skin-Effekt bezeichnet man die Erscheinung, dass sich mit steigender Frequenz der Elektronenstrom mehr und mehr zur Oberfläche eines Leiters hin verlagert. Dadurch erhöht sich mit steigender Frequenz der ohmsche Leiterwiderstand. | |
| Als Skin-Effekt bezeichnet man die Erscheinung, dass sich mit steigender Frequenz die Induktivität und die Kapazität eines Leiters erhöht. Dadurch erhöht sich mit steigendem Leiterwiderstand die Resonanzfrequenz. | |
| Als Skin-Effekt bezeichnet man die Erscheinung, dass sich mit steigender Frequenz der Elektronenstrom mehr und mehr zur Leitermitte hin verlagert. Dadurch erhöht sich der ohmsche Leiterwiderstand bei hohem Wechselstromanteil. | |
Ohmsches Gesetz, Leistung
Um einen Widerstand berechnen zu können, benötigt man die Spannung am Widerstand und den Strom durch den Widerstand. Dann gilt nach dem ohmschen Gesetz \[ R = \frac{U}{I} \ \ \text{oder umgestellt} \ \ U = R \cdot I \] Eselsbrücken: Sie kennen R-u-d-i? R= U durch I oder den Schweizer Kanton URI? Schauen Sie auch im Kapitel 1 nach dem URI-Dreieck!
Allerdings gilt dieser einfache Zusammenhang nur, wenn Strom und Spannung in Phase sind. Wenn Kondensatoren oder Spulen in der Schaltung enthalten sind, treten Phasenverschiebungen zwischen Spannung und Strom auf. Die Berechnung muss dann den Phasenwinkel berücksichtigen. Man nennt es auch eine "geometrische" Berechnung oder Rechnungen mit "Vektoren". Diese kommen in der Prüfung für das Amateurfunkzeugnis nicht vor.
ehemalige Prüfungsfrage
| TC101 Welche Schaltung könnte dazu verwendet werden, den Wert eines Widerstandes anhand des ohmschen Gesetzes zu ermitteln? | |
|---|---|
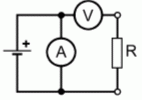 | |
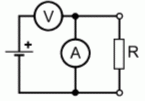 | |
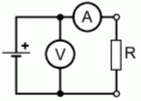 | |
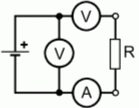 | |
Die Toleranz
Im Kapitel 4 (Lektion 4) im Buch zur Klasse E wird das Toleranzschema ausführlich dargestellt. In der Prüfung Klasse A gibt es dazu nur eine Prüfungsfrage.
ehemalige Prüfungsfrage
| TC109 Ein Widerstand hat eine Toleranz von 10 %. Bei einem nominalen Widerstandswert von 5,6 kΩ liegt der tatsächliche Wert zwischen | |
|---|---|
| 5040 und 6160 Ω. | |
| 4760 und 6440 Ω. | |
| 4,7 und 6,8 kΩ. | |
| 5,2 und 6,3 kΩ. | |
Lösungsweg (hier klicken zum Anzeigen):
Aufbau von Widerständen
Beim Aufbau von Widerständen unterscheidet man Kohleschichtwiderstände, Metallschichtwiderstände, Metalloxidwiderstände und Drahtwiderstände. Im Amateurfunklehrgang zur Klasse E, Kapitel 4 sind die Eigenschaften genauer beschrieben.
Zusammenfassung: Kohleschichtwiderstände sind billig, haben aber eine relativ große Herstellungstoleranz. Metallschichtwiderstände sind Präzisionswiderstände. Metalloxidwiderstände eignen sich besonders für Hochfrequenz. Drahtwiderstände eignen sich als Hochlastwiderstände bei niedrigen Frequenzen (Niederfrequenzbereich).
ehemalige Prüfungsfrage
| TC102 Metallschichtwiderstände | |
|---|---|
| haben geringe Fertigungstoleranzen und Temperaturabhängigkeit und sind besonders als Präzisionswiderstände geeignet. | |
| sind induktionsarm und eignen sich besonders für den Einsatz bei sehr hohen Frequenzen. | |
| sind besonders als Hochlastwiderstände bei niedrigen Frequenzen geeignet. | |
| haben einen extrem stark negativen Temperaturkoeffizienten und sind besonders als NTC-Widerstände (Heißleiter) geeignet. | |
ehemalige Prüfungsfrage
| TC103 Metalloxidwiderstände | |
|---|---|
| haben geringe Toleranzen und Widerstandsänderungen und sind besonders als Präzisionswiderstände in der Messtechnik geeignet. | |
| sind besonders als Hochlastwiderstände bei niedrigen Frequenzen geeignet. | |
| sind induktionsarm und eignen sich besonders für den Einsatz bei sehr hohen Frequenzen. | |
| haben einen extrem stark negativen Temperaturkoeffizienten und sind besonders als NTC-Widerstände (Heißleiter) geeignet. | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TC104 Drahtwiderstände | |
|---|---|
| Drahtwiderstände werden hauptsächlich in Form von SMD-Widerständen hergestellt. | |
| sind induktionsarm und eignen sich besonders für den Einsatz bei sehr hohen Frequenzen. | |
| haben einen extrem stark negativen Temperaturkoeffizienten und sind besonders als NTC-Widerstände (Heißleiter) geeignet. | |
| sind besonders als Hochlastwiderstände bei niedrigen Frequenzen geeignet. | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TC112 Ein Lastwiderstand besteht aus zwölf parallel geschalteten 600-Ω-Drahtwiderständen. Er eignet sich höchstens | |
|---|---|
| für Funkfrequenzen bis etwa 144 MHz. | |
| für UHF-Senderausgänge mit 50 Ω. | |
| für Tonfrequenzen bis etwa 15 kHz. | |
| als Langdrahtersatz. | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TC113 Eine künstliche Antenne für den VHF-Bereich könnte beispielsweise aus | |
|---|---|
| hochbelastbaren Drahtwiderständen zusammengebaut sein. | |
| ungewendelten Kohleschichtwiderständen zusammengebaut sein. | |
| Glühbirnen zusammengebaut sein. | |
| temperaturfesten Blindwiderständen bestehen. | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TC114 Welche der folgenden Bauteile könnten für eine genaue künstliche Antenne, die bei 50 MHz eingesetzt werden soll, verwendet werden? | |
|---|---|
| 10 Kohleschichtwiderstände von 500 Ω | |
| ein 50-Ω-Drahtwiderstand | |
| 2 parallel geschaltete Drahtwiderstände von 100 Ω | |
| ein Spulenanpassfilter im Ölbad | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TC115 Aus welchen Bauteilen sollte eine künstliche Antenne für den VHF-Bereich gebaut werden? | |
|---|---|
| Aus Drahtwiderständen mit kapazitätsarmen Anschlusskappen | |
| Aus einem abgestimmten Topfkreis mit induktiver Einkopplung | |
| Aus versilberten Kupfer-Rundstäben von 10 mm Durchmesser | |
| Aus induktionsarmen Kohleschichtwiderständen | |
Lösungsweg (hier klicken zum Anzeigen):
Der Innenwiderstand
Für Netzteile zur Spannungsversorgung von Geräten benutzt man Spannungsquellen, die einen sehr geringen Innenwiderstand haben sollen, damit die Spannung konstant bleibt. Zum Laden von Akkus wird gelegentlich eine Stromquelle gebraucht, bei der der Strom konstant bleiben soll. Dies geht nur bei großem Innenwiderstand oder besser ausgedrückt, wenn der Innenwiderstand der Spannungsquelle viel größer ist als der Lastwiderstand. In diesem Zusammenhang folgen einige Aufgaben zum Thema Leistungsanpassung, Stromanpassung, Spannungsanpassung.
ehemalige Prüfungsfrage
| TB210 Welche Eigenschaften sollten Strom- und Spannungsquellen aufweisen? | |
|---|---|
| Strom- und Spannungsquellen sollten einen möglichst niedrigen Innenwiderstand haben. | |
| Spannungsquellen sollten einen möglichst niedrigen Innenwiderstand und Stromquellen einen möglichst hohen Innenwiderstand haben. | |
| Strom- und Spannungsquellen sollten einen möglichst hohen Innenwiderstand haben. | |
| Spannungsquellen sollten einen möglichst hohen Innenwiderstand und Stromquellen einen möglichst niedrigen Innenwiderstand haben. | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB202 Die Leerlaufspannung einer Gleichspannungsquelle beträgt 13,5 V. Wenn die Spannungsquelle einen Strom von 0,9 A abgibt, sinkt die Klemmenspannung auf 12,4 V. Wie groß ist der Innenwiderstand der Spannungsquelle? | |
|---|---|
| 0,82 Ω | |
| 1,1 Ω | |
| 1,22 Ω | |
| 12,15 Ω | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB203 Die Leerlaufspannung einer Gleichspannungsquelle beträgt 13,5 V. Wenn die Spannungsquelle einen Strom von 2 A abgibt, sinkt die Klemmenspannung auf 13 V. Wie groß ist der Innenwiderstand der Spannungsquelle? | |
|---|---|
| 13 Ω | |
| 6,75 Ω | |
| 0,5 Ω | |
| 0,25 Ω | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB206 Die Leerlaufspannung einer Gleichspannungsquelle beträgt 5 V. Schließt man einen Belastungswiderstand mit 1,2 Ohm an, geht die Klemmenspannung der Spannungsquelle auf 4,8 Volt zurück. Wie groß ist der Innenwiderstand der Spannungsquelle? | |
|---|---|
| 0,2 Ω | |
| 0,25 Ω | |
| 0,05 Ω | |
| 8,2 Ω | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB204 Die Leerlaufspannung einer Gleichspannungsquelle beträgt 13,5 V. Wenn die Spannungsquelle einen Strom von 1 A abgibt, sinkt die Klemmenspannung auf 12,5 V. Wie groß ist der Wirkungsgrad der Spannungsquelle? | |
|---|---|
| 7,5 % | |
| 13,5 % | |
| 92,6 % | |
| 100 % | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB205 Die Leerlaufspannung einer Gleichspannungsquelle beträgt 13,5 V. Wenn die Spannungsquelle einen Strom von 2 A abgibt, sinkt die Klemmenspannung auf 13 V. Wie groß ist der Wirkungsgrad? | |
|---|---|
| 96,3 % | |
| 100 % | |
| 3,7 % | |
| 27 % | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB207 In welchem Zusammenhang müssen Innenwiderstand Ri und Lastwiderstand RL stehen, damit Leistungsanpassung vorliegt? | |
|---|---|
| \( R_L = R_i \) | |
| \( R_L \gg R_i \) | |
| \( R_L \ll R_i \) | |
| \( R_L = \frac{1}{R_i} \) | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB209 In welchem Zusammenhang müssen Innenwiderstand Ri und Lastwiderstand RL stehen, damit Spannungsanpassung vorliegt? | |
|---|---|
| \( R_L = R_i \) | |
| \( R_L \gg R_i \) | |
| \( R_L \ll R_i \) | |
| \( R_L = \frac{1}{R_i} \) | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB208 In welchem Zusammenhang müssen Innenwiderstand Ri und Lastwiderstand RL stehen, damit Stromanpassung vorliegt? | |
|---|---|
| \( R_L = R_i \) | |
| \( R_L \gg R_i \) | |
| \( R_L \ll R_i \) | |
| \( R_L = \frac{1}{R_i} \) | |
Lösungsweg (hier klicken zum Anzeigen):
Die elektrische Leistung
Aus dem Amateurfunklehrgang Klasse E wissen Sie, dass Leistung das Produkt ist aus Spannung und Strom.
\[ P = U \cdot I \]Für Wechselspannung/Wechselstrom an einem Widerstand gilt diese Formel auch, wenn entsprechende Effektivwerte eingesetzt werden. Die Formel gilt nicht, wenn die Last Kondensatoren oder Spulen enthält. Dann treten Phasenverschiebungen zwischen Spannung und Strom auf, die bei der Berechnung der Leistung berücksichtigt werden müssen. Die Berechnung wird schwierig. Dies ist nicht Gegenstand der Prüfung für das Amateurfunkzeugnis.
Nur eine Frage ist enthalten, nämlich die Leistung zu berechnen, wenn nur ein Kondensator angeschlossen ist. Ein Kondensator wird bei Wechselstrom nur kurz aufgeladen und dann wieder entladen und danach umgekehrt aufgeladen. Dabei wird keine Leistung abgegeben. Der Kondenstor gibt diese immer wieder zurück. Nur ganz geringe Umladeverluste entstehen, die praktisch vernachlässigbar sind.
ehemalige Prüfungsfrage
| TB913 An einem Kondensator mit einer Kapazität von 1 µF wird eine NF-Spannung von 10 kHz und 12 Veff angelegt. Wie groß ist die aufgenommene Wirkleistung im eingeschwungenen Zustand? | |
|---|---|
| Fast null Watt | |
| 0,9 Watt | |
| 0,75 Watt | |
| 9 Watt | |
Lösungsweg (hier klicken zum Anzeigen):
Es sind viele Aufgaben zum Thema Leistung im Prüfungsfragenkatalog enthalten, wobei alle umgestellten Formeln in der Formelsammlung stehen. Man muss wissen, dass Belastbarkeit eines Widerstandes maximale Leistung bedeutet.
ehemalige Prüfungsfrage
| TC107 Welche Belastbarkeit muss ein Vorwiderstand haben, an dem bei einem Strom von 48 mA eine Spannung von 208 V abfallen soll? | |
|---|---|
| 0,5 W | |
| 4,8 W | |
| 10 W | |
| 100 W | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TC108 Ein Widerstand von 120 Ω hat eine Belastbarkeit von 23 Watt. Welcher Strom darf höchstens durch den Widerstand fließen, damit er nicht überlastet wird? | |
|---|---|
| 192 mA | |
| 438 mA | |
| 43,7 mA | |
| 2,28 A | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TC111 Ein Oszilloskop zeigt einen sinusförmigen Spitze-Spitze-Wert von 25 V an einem 1000-Ω-Widerstand an. Der Effektivstrom durch den Widerstand beträgt | |
|---|---|
| 8,8 mA. | |
| 12,5 mA. | |
| 25 mA. | |
| 40 A. | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB914 Welche Belastbarkeit muss ein 100-Ohm-Widerstand, an dem 10 Volt anliegen, mindestens haben? | |
|---|---|
| 100 mW | |
| 0,125 W | |
| 1 W | |
| 10 W | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB916 Der Effektivwert der Spannung an einer künstlichen 50-Ohm-Antenne wird mit 100 V gemessen. Die Leistung an der Last beträgt | |
|---|---|
| 100 W. | |
| 141 W. | |
| 200 W. | |
| 283 W. | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB917 Eine künstliche 50-Ohm-Antenne (dummy load) besteht aus elf 560-Ohm-Widerständen mit einem Belastungsnennwert von je 5 Watt. Wie hoch ist die zulässige Gesamtleistung, die angelegt werden darf? | |
|---|---|
| 5 W | |
| 27,5 W | |
| 55 W | |
| 750 W | |
Lösungsweg (hier klicken zum Anzeigen):
Leistungsformel umstellen
Es folgen drei Aufgaben, bei denen die Leistungsformel \[ P =\frac{U^2}{R} \] nach U oder \[ P = I^2 \cdot R \] nach I umgestellt werden muss. Das Umstellen dieser Formeln wurde bereits im vorigen Kapitel 1 geübt.
ehemalige Prüfungsfrage
| TB922 An einem Widerstand R wird die elektrische Leistung P in Wärme umgesetzt. Sie kennen die Größen P und R. Nach welcher der Formeln können Sie die Spannung ermitteln, die an dem Widerstand R anliegt? | |
|---|---|
| \( U = R \cdot P \) | |
| \( U = \sqrt{P \cdot R} \) | |
| \( U = \sqrt{\frac{P}{R}} \) | |
| \( U = \frac{P}{R} \) | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB923 In welcher Antwort sind alle dargestellten Zusammenhänge zwischen Strom, Spannung, Widerstand und Leistung richtig? | |
|---|---|
| \( I = \sqrt{ P \cdot R} \ ; \ \ U = \sqrt{\frac{P}{R}} \) | |
| \( I = \sqrt{\frac{R}{P}} \ ; \ \ U = \sqrt{P \cdot R} \) | |
| \( I = \sqrt{\frac{P}{R}} \ ; \ \ U = \sqrt{P \cdot R} \) | |
| \( I = \frac{\sqrt{P}}{R} \ ; \ \ U = \sqrt{P} \cdot R \) | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB924 In welcher Antwort sind alle dargestellten Zusammenhänge zwischen Widerstand, Leistung, Spannung und Strom richtig? | |
|---|---|
| \( R = U^2 \cdot P \ ; \ \ R = \frac{P}{I^2}\) | |
| \( R = \frac{P}{U^2} \ ; \ \ R = P \cdot I^2 \) | |
| \( R = \frac{U^2}{P} \ ; \ \ R = P \cdot I^2 \) | |
| \( R = \frac{U^2}{P} \ ; \ \ R = \frac{P}{I^2} \) | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TC105 Ein Widerstand von 10 kΩ hat eine maximale Spannungsfestigkeit von 0,7 kV und eine maximale Belastbarkeit von einem Watt. Welche Gleichspannung darf höchstens an den Widerstand angelegt werden ohne ihn zu überlasten? | |
|---|---|
| 1 V | |
| 10 V | |
| 0,1 kV | |
| 700 V | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TC106 Ein Widerstand von 50 kΩ hat eine maximale Spannungsfestigkeit von 0,7 kV und eine maximale Belastbarkeit von 2 Watt. Welche Gleichspannung darf höchstens an den Widerstand angelegt werden ohne ihn zu überlasten? | |
|---|---|
| 25 V | |
| 100 V | |
| 316 V | |
| 700 V | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB915 Eine Glühlampe hat einen Nennwert von 12 V und 48 W. Wie hoch ist die Stromentnahme bei einer 12-V-Versorgung? | |
|---|---|
| 250 mA | |
| 750 mA | |
| 4 A | |
| 36 A | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB919 Ein HF-Verstärker ist an eine 12,5-V-Gleichstromversorgung angeschlossen. Wenn die HF-Ausgangsleistung des Verstärkers 90 W beträgt, zeigt das an die Stromversorgung angeschlossene Amperemeter 16 A an. Der Wirkungsgrad des Verstärkers beträgt | |
|---|---|
| 45 %. | |
| 55 %. | |
| 100 %. | |
| 222 %. | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB921 Ein Spannungsmesser und ein Amperemeter werden für die Ermittlung der Gleichstromeingangsleistung einer Schaltung verwendet. Der Spannungsmesser zeigt 10 V, das Amperemeter 10 A an. Falls beide dabei im Rahmen ihrer Messgenauigkeit jeweils einen um 5 % zu geringen Wert anzeigen würden, würde man die elektrische Leistung um ... | |
|---|---|
| 5 % zu niedrig bestimmen. | |
| 5 % zu hoch bestimmen. | |
| 9,75 % zu niedrig bestimmen. | |
| 10,25 % zu hoch bestimmen. | |
Lösungsweg (hier klicken zum Anzeigen):
Reihenschaltung von Widerständen
Im Lehrgang für Klasse E wurden im Kapitel 4 recht ausführlich die Reihen- und Parallelschaltung von Widerständen, sowie einfache gemischte Schaltungen und deren Berechnung behandelt. Allerdings waren es einfachere gemischte Schaltungen als manche hier aus dem Fragenkatalog für Klasse A. Hier noch einmal die Übersicht:

Bei einer Reihenschaltung sind die Widerstände hintereinander geschaltet. Der Gesamtwiderstand ist ganz einfach die Summe der Einzelwiderstände. \[ \boxed{ R = R_1 + R_2 + R_3 + \ldots} \] Ferner wissen Sie aus dem Kapitel 4 Klasse E, dass sich bei einer Reihenschaltung die Spannungen wie die Widerstände verhalten. Ist bei einer Reihenschaltung ein Widerstand beispielsweise fünfmal so groß wie ein anderer, muss auch die Spannung an diesem Widerstand fünfmal so groß sein.
ehemalige Prüfungsfrage
| TD108 Wie teilt sich die Spannung an zwei in Reihe geschalteten Widerständen auf, wenn R1 = 5 mal so groß ist wie R2 ? | |
|---|---|
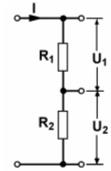 | |
| \( \large U_1 = 5 \cdot U_2 \) | |
| \( \large U_1 = 6 \cdot U_2 \) | |
| \( \large U_1 = \frac{U_2}{5} \) | |
| \( \large U_1 = \frac{U_2}{6} \) | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TD109 Wie teilt sich die Spannung an zwei in Reihe geschalteten Widerständen auf, wenn R1 \( \frac{1}{6} \) mal so groß ist wie R2 ? | |
|---|---|
 | |
| \( \large U_1 = 5 \cdot U_2 \) | |
| \( \large U_1 = 6 \cdot U_2 \) | |
| \( \large U_1 = \frac{U_2}{5} \) | |
| \( \large U_1 = \frac{U_2}{6} \) | |
Lösungsweg (hier klicken zum Anzeigen):
Parallelschaltung von Widerständen
Die Formel für die Parallelschaltung von Widerständen lautet \[ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots \] Wenn nur zwei Widerstände parallel geschaltet sind, vereinfacht sich die Formel zu \[ \boxed{\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}} \] Wie im vorigen Kapitel gezeigt wurde, lässt sich diese Formel auch umstellen zu \[ \boxed{R = \frac{R_1 \cdot R_2}{R_1 + R_2}} \] Mit welcher der beiden Formeln gerechnet wird, ist "Geschmacksache". Wenn man einen Taschenrechner mit \( \large \frac{1}{x} \)-Taste hat, ist die obere Formel einfacher zu handhaben. Dies zeige ich Ihnen am Beispiel der Prüfungsaufgabe TD103.
ehemalige Prüfungsfrage
| TD101 Wie groß ist der Gesamtwiderstand dieser Schaltung, wenn R1 = 3,3 kΩ, R2 = 4,7 kΩ und R3 = 27 kΩ betragen? | |
|---|---|
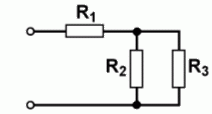 | |
| 1,8 kΩ | |
| 4,0 kΩ | |
| 7,3 kΩ | |
| 35 kΩ | |
ehemalige Prüfungsfrage
| TD121 Wenn R1 und R3 je 2 kΩ hat und R2 und R4 je 200 Ω betragen, hat die Schaltung einen Gesamtwiderstand von … | |
|---|---|
 | |
| 1100 Ω | |
| 2200 Ω | |
| 4400 Ω | |
| 2,2 kΩ | |
Lösungsweg (hier klicken zum Anzeigen):
Wenn drei Widerstände parallel geschaltet sind, rechnet man nach der Formel \[ \boxed{ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots } \] obwohl es auch eine nach R aufgelöste Formel für drei Widerstände gibt. Sie lautet \[ \boxed{R = \frac{R_1 \cdot R_2 \cdot R_3}{R_1 \cdot R_2 + R_1 \cdot R_3 + R_2 \cdot R_3}} \]
ehemalige Prüfungsfrage
| TD123 Wie groß ist der Gesamtwiderstand dieser Schaltung, wenn R1 = 30 kΩ, R2 = 15 kΩ, R3 = 30 kΩ und R4 = 2,7 kΩ betragen? | |
|---|---|
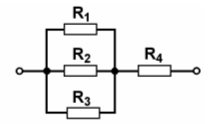 | |
| 4,5 kΩ | |
| 10,2 kΩ | |
| 12,7 kΩ | |
| 82,7 kΩ | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TD124 Wie groß ist der Gesamtwiderstand dieser Schaltung, wenn R1 = 12 kΩ, R2 = 12 kΩ, R3 = 6 kΩ und R4 = 1,5 kΩ betragen? | |
|---|---|
 | |
| 4,5 kΩ | |
| 10,2 kΩ | |
| 31,5 kΩ | |
| 5,5 kΩ | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TD114 Drei gleich große parallel geschaltete Widerstände haben einen Gesamtwiderstand von 1,67 kΩ. Welchen Wert hat jeder Einzelwiderstand? | |
|---|---|
| 557 Ω | |
| 10,0 kΩ | |
| 5,0 kΩ | |
| 2,5 kΩ | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TD115 Welche Belastbarkeit kann die Zusammenschaltung von drei gleich großen Widerständen mit einer Einzelbelastbarkeit von je 1 W erreichen, wenn alle 3 Widerstände entweder parallel oder in Reihe geschaltet werden? | |
|---|---|
| 1 W bei Parallel- und bei Reihenschaltung. | |
| 3 W bei Parallel- und 1 W bei Reihenschaltung. | |
| 1 W bei Parallel- und 3 W bei Reihenschaltung. | |
| 3 W bei Parallel- und bei Reihenschaltung. | |
Lösungsweg (hier klicken zum Anzeigen):
Gemischte Schaltungen
Bei gemischten Schaltungen von vielen Widerständen gilt folgendes Prinzip. Suchen Sie zunächst die Widerstände heraus, die entweder eindeutig in Reihe oder eindeutig parallel geschaltet sind und ersetzen Sie diese durch den berechneten Ersatzwiderstand.
ehemalige Prüfungsfrage
| TD107 Wie groß ist der Gesamtwiderstand der dargestellten Schaltung? | |
|---|---|
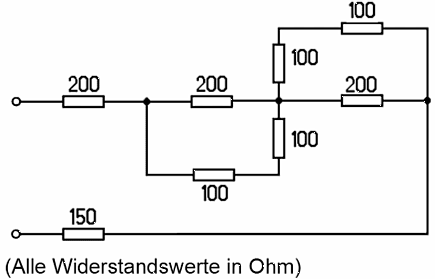 | |
| 360 Ω | |
| 383 Ω | |
| 1150 Ω | |
| 550 Ω | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TD122 In welchem Bereich bewegt sich der Eingangswiderstand der folgenden Schaltung, wenn R alle Werte von 0 bis unendlich durchläuft? | |
|---|---|
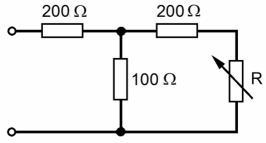 | |
| 100 bis 200 Ω | |
| 200 bis 400 Ω | |
| 300 bis 366,7 Ω | |
| 266,7 bis 300 Ω | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TD112 Wie groß ist der Strom durch R3, wenn U = 15 V und alle Widerstände R1 bis R3 je 10 kΩ betragen? | |
|---|---|
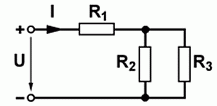 | |
| 0,5 mA | |
| 1,0 mA | |
| 1,6 mA | |
| 4,5 mA | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TD113 Welche Leistung tritt an R2 auf, wenn U = 15 V und alle Widerstände R1 bis R3 je 10 kΩ betragen? | |
|---|---|
 | |
| 0,15 W | |
| 2,5 mW | |
| 1,5 mW | |
| 5,0 mW | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TD111 Wie groß ist die Spannung U, wenn durch R3 ein Strom von 1 mA fließt und alle Widerstände R1 bis R3 je 10 kΩ betragen? | |
|---|---|
 | |
| 15 V | |
| 20 V | |
| 30 V | |
| 40 V | |
Lösungsweg (hier klicken zum Anzeigen):
Viel Erfolg beim Lehrgang wünscht Ihnen Eckart Moltrecht DJ4UF!
Zur Lehrgangs-Übersicht Technik Klasse A
| Copyright-Hinweis: | |
|---|---|
 | Dieser DARC-Online-Lehrgang wurde mit freundlicher Genehmigung des Autors Eckart K. W. Moltrecht aus seinen Büchern "Amateurfunk-Lehrgang für das Amateurfunkzeugnis" aus dem VTH-Verlag (möglicherweise einer älteren Auflage!) für das Internet umgewandelt. Das Copyright liegt beim Autor und beim Verlag. Mehr über den Autor! |
 | Die Darstellung auch nur von Auszügen oder Zeichnungen oder Fotos im Internet ist untersagt. Für die private Verwendung können Sie gern eine Genehmigung beim Autor erhalten. Schreiben Sie eine E-Mail an eckart.moltrecht(at)gmail.com! |
Letzte Bearbeitung: 16.06.2017 DJ4UF, 04.04.2020 DH8GHH
Fehlermeldungen mit Linkangabe an DH8GHH@darc.de

