Die Dämpfung auf Kabeln mit dem Begriff Dezibel ist ein sehr wichtiges Kapitel nicht nur im Amateurfunk, sondern in der gesamten Hochfrequenztechnik.

Inhaltsübersicht

• Dämpfungsfaktor
• Dämpfungsmaß dB
• Verstärkung in dB
• Spannungsdämpfungsmaß
• Pegel
• Wellenwiderstand
• Dämpfungsberechnung
• Anpassung
• Stehwellenverhältnis
• Symmetrierung
• Stecker und Adapter

Das Dezibel ist eine Zusammenziehung von Bel und einem Zehntel davon - dezi. Sie kennen sicher ein Dezimeter. Das ist ein Zehntel Meter, also 10 Zentimeter. Aber nun: Bel – was ist das?

Der Dämpfungsfaktor

Der Dämpfungsfaktor D gibt das Verhältnis der am Anfang einer übertragungsstrecke vorhandenen Leistung P₁ zu der am Ende übrig gebliebenen Leistung P₂ an.

\[ D_P = \frac{P_1}{P_2} \]

Der Dämpfungsfaktor ist ein reiner Zahlenwert. D_P = 10 bedeutet, dass die Leistung am Anfang zehnmal höher ist als am Ende des Kabels.

Hat man in einer übertragungsstrecke viele Einzeldämpfungen zu berücksichtigen, muss man die Einzelfaktoren miteinander multiplizieren, um den Gesamtdämpfungsfaktor zu erhalten.

Aufgabe

Berechnen Sie die Einzeldämpfungen zwischen den verschiedenen Anschlusspunkten in Bild 10-1 und multiplizieren Sie diese anschließend zum Gesamtdämpfungsfaktor.

D₁ = 10 : 8 = 1,25;  D₂ = 8 : 5 = 1,6 und so weiter. Dann D₁ · D₂ · D₃ · D₄ = ..... Führen Sie die Probe durch, indem Sie den Gesamt­dämpfungsfaktor aus P₁ und P₅ berechnen.

Dämpfungsmaß dB

Einfacher kann man die Einzeldämpfungen zu einer Gesamtdämpfung zusammenfassen, wenn man die einzelnen Zahlenwerte nur zu addieren braucht. Dies erreicht man durch die Rechnung mit dem Dezibel, das aus der Logarithmenrechnung abgeleitet wurde. In der Mathematik gilt

\[ \lg \left( a \cdot b \cdot c \right) = \lg a + \lg b + \lg c \]

Aus einer Multiplikation wird durch den Logarithmus eine Addition. Man muss also nur den Logarithmus der Einzeldämpfungen kennen und kann dann die Zahlenwerte addieren. Diese Rechnung führt zum Dämpfungsmaß, ausgedrückt in Bel bzw. Dezibel (gesprochen: dezi-behl). Man definiert das Leistungsdämpfungsmaß als

\[ a_P = \lg \frac{P_1}{P_2} \text{Bel} \]

1 Bel = 10 dB(Dezibel)

\[ a_P = 10 \cdot \lg \frac{P_1}{P_2} \text{dB} \]

P₁ = Eingangsleistung, P₂ = Ausgangsleistung

Diese Formeln bedeuten: Wenn man von dem Verhältnis zweier Leistungen den Logarithmus berechnet, erhält man einen Zahlenwert, den man dann als Wert in Bel bezeichnet. Weil das Bel eine relativ große Einheit ist, wählt man in der Praxis das Dezibel, weil man dann Zahlenwerte zwischen 0,1 und 100 erhält.

Beispiel

Anhand folgenden Beispiels wird gezeigt, wie man mit Hilfe eines Taschenrechners eine solche Dämpfung in Dezibel berechnet. Es soll das Dämpfungsmaß von Punkt 1 nach Punkt 5 aus den Einzeldämpfungs­maßen berechnet werden.

Lösung: Die Dämpfung von Punkt 1 nach Punkt 2 (Kabel 1) wird zuerst berechnet. Zunächst werden die Werte in die Formel eingesetzt.

\[ a_P = 10 \cdot \lg \frac{10}{8} \text{dB} \]

Zur Eingabe in den Taschenrechner gehen Sie gemäß folgender Tabelle vor.

Eingabe	Anzeige
10	10
/
8	8
=	1.25
LOG	9.691...-02
*
10	10
=	0.9691...

Als Ergebnis erhalten Sie den Wert 0,9691. Das Dämpfungsmaß beträgt also gerundet a₁  = 1 dB. Für die weiteren Dämpfungsmaße ergeben sich a₂  = 2 dB, a₃  = 1 dB und a₄  = 2 dB. Die Gesamtdämpfung durch Addition dieser Werte beträgt 6 dB.

Probe:

\[ a_P = 10 \cdot \lg \frac{10}{2,5} \text{dB} = \mathbf{6 \ dB} \]

Dämpfungswerte in Dezibel lassen sich addieren. Hat man beispielsweise ein Stück Kabel mit 1,5 dB und ein dazu ein zweites mit 1 dB Dämpfung, ergeben sich zusammen 2,5 dB. Dies ist der Hauptvorteil der Rechnung mit Dezibel.

Verstärkung in dB

In der Sendertechnik und hat man es anstatt mit Dämpfungen mit Verstärkungen zu tun. Die Ausgangsleistung ist dabei größer als die Eingangsleistung. Dies gilt auch für den Gewinn (gain, g) einer Antenne (siehe Kapitel 11 in diesem Lehrgang). Dann rechnet man eine Verstärkung in dB nach folgender Formel:

\[ g = 10 \cdot \lg \frac{P_2}{P_1} \text{dB} \]

also Ausgangsleistung geteilt durch Eingangsleistung.

Beispiel

Eine Endstufe verstärkt eine Leistung von 1 Watt auf 4 Watt. Wie groß ist die Verstärkung in dB?

Lösung: 4 geteilt durch 1 ist 4. Nehmen Sie den Logarithmus davon, ergibt 0,602. Multiplizieren Sie mit 10, ergibt 6,02. Also: Die Verstärkung beträgt zirka 6 dB.

Rechnen Sie "zum Spaß" einmal umgekehrt, also 1 geteilt durch 4 und so weiter. Ihr Taschenrechner wird -6,02 anzeigen. Wenn also die Eingangsleistung 4 Watt wäre (am Anfang einer Leitung) und am Ausgang 1 Watt, ergäbe sich eine "Verstärkung" von -6 dB.

Dämpfung ist negative Verstärkung.

Man kann also "Gewinn" und "Verlust" in einer Aufgabe zusammenrechnen, indem man alle Gewinne (Verstärkungen) positiv und alle Dämpfungen negativ rechnet.

Übungsaufgabe
Eine Antennenanlage hat ein Kabel mit 1 dB Dämpfung und verwendet eine Richtantenne mit 11 dB Gewinn. Wie groß ist der verbleibende "Gewinn"?

Lösung
Gesamtgewinn = -1 dB + 11 dB = 10 dB

Aufgabe
Berechnen Sie weitere Verstärkungsmaße in dB, wenn gemäß folgender Tabelle die Leistungen gegeben sind und tragen Sie die Ergebnisse in die Tabelle ein, bzw. Überprüfen Sie Ihre Lösung.

Eingang	Ausgang	Lösung
1 W	4 W
1 W	10 W
1 W	100 W
1 W	2 W
1 W	1,41 W

Aus dieser Tabelle sollten Sie sich ein paar Zahlenwerte merken, nämlich: vierfache Leistung ergibt 6 dB, zehnfacher Leistung entspricht 10 dB, hundertfacher Leistung entspricht 20 dB, doppelter Leistung entspricht 3 dB und √2-facher Leistung entspricht 1,5 dB.

In folgender Tabelle sind noch einmal die wichtigsten Werte zusammengestellt. Wichtig sind diese, weil sie in den Prüfungsaufgaben vorkommen.

dB Wert	Leistungsfaktor
0	1
1,5	\( \sqrt{2} = 1{,}41 \)
2,15	1,64
3	2
6	4
10	10
20	100

Den Wert 2,15 dB benötigen wir später, um in Kapitel 18 den Gewinn einer Dipolantenne gegenüber einem Kugelstrahler berechnen zu können. Mit diesen wenigen Werten können wir nun auch andere Dämpfungsmaße durch Zusammensetzung ermitteln.

Zusammengesetzte Werte

Wenn Sie die Umrechnungsfaktoren für die wichtigsten dB-Werte kennen, können Sie durch Zusammensetzungen auch andere ermitteln. Dazu muss man nur wissen, dass ein positiver dB-Wert der Multiplikation (malnehmen) und ein negativer der Division (teilen) entspricht. Angenommen, Sie wissen, dass 3 dB doppelter Leistung und 10 dB zehnfacher Leistung entspricht.

Beispiel: Welchem Leistungsfaktor entsprechen 26 dB?

Lösung :
10 dB + 10 dB + 3 dB + 3 dB = 26 dB
10    · 10    · 2    · 2    = 400

Beispiel: Welchem Leistungsfaktor entsprechen 27 dB?

Lösung :
10 dB + 10 dB + 10 dB - 3 dB = 27 dB
10    · 10    · 10    : 2    = 500

Beispiel: Welchem Leistungsfaktor entsprechen 14 dB?

Lösung :
10 dB + 10 dB - 3 dB - 3 dB = 14 dB
10    · 10    : 2    : 2    = 25

Wir prüfen den letzten Wert einmal durch Rechnung mit der Formel nach.

\[ g = 10 \cdot \lg \frac{P_2}{P_1} \text{dB} \]

P₁ /P₂ ist der Leistungsfaktor 25.

\[ g = 10 \cdot lg 25 \text{dB} = \mathbf{14 \ dB} \]

Das Spannungsdämpfungsmaß

Die Definition des Dezibels geht vom Leistungsverhältnis aus. Dies sollten Sie sich merken! Das Verhältnis von Spannungen kann man ebenfalls in dB umrechnen. Die Prüfungsaufgaben zum Amateurfunkzeugnis Klasse E enthalten nur Rechnungen mit Leistungen. Die Zusammenhänge in Bezug auf Spannungen werden deshalb hier nur kurz angesprochen, weil es in der Praxis damit immer wieder Verwechslungen gibt.

Wenn man an einem Kabel oder an einem Verstärker am Eingang und am Ausgang nur die Spannung misst, kann man unter der Voraussetzung, dass die Eingangs- und Ausgangswiderstände gleich sind, mit folgender Formel die Dämpfung beziehungsweise die Verstärkung in dB ausrechnen. Die Ableitung dieser Formel finden Sie im Aufbaulehrgang zur Klasse A.

\[ a_U = 20 \cdot \lg \frac{U_1}{U_2} \text{dB} \]

a_u steht für den Spannungsdämpfungsfaktor, U₁ und U₂ für die Eingangs- und Ausgangsspannung. Statt einer 10 bei Leistungen steht hier die 20 vor dem Logarithmus. Deshalb sind die Dezibelwerte bei gleichem Verhältnis doppelt so hoch. Vergleichen Sie die beiden folgenden Tabellen!

Leistungsfaktor	Dezibel
2	3 dB
4	6 dB
10	10 dB

Spannungsfaktor	Dezibel
2	6 dB
4	12 dB
10	20 dB

Die S-Stufen im Amateurfunk

Eine weitere Anwendung der dB-Rechnung sind die „S-Stufen“ bei der Empfangsbeurteilung im Amateurfunk. In der Empfangstechnik hat man bei der Angabe der Empfangsfeldstärke im RST-System für die Lautstärke S9 einen bestimmten Wert einer Empfangsspannung an einem 50-Ohm-Eingang festgelegt.

Kurzwelle : S9 entspricht 50 µV an 50 Ω
UKW : S9 entspricht 5 µV an 50 Ω

Jede der neun S-Stufen entspricht 6 dB. 6 dB entsprechen einem Faktor 2 bei Spannungen, S8 hat also bei Kurzwelle einen Wert von 25 µV, S1 von 0,2 µV. S0 gibt es nicht.

	S9	S8	S7	S6	S5	S4	S3	S2	S1
KW	50	25	12,5	6,25	3,12	1,56	0,78	0,39	0,2
UKW	5	2,5	1,25	0,62	0,31	0,16	0,80	0,04	0,02

Tabelle der S-Werte in µV

Um auch Empfangsspannungen größer als 50 µV (bzw. 5 µV bei UKW) im RST-System angeben zu können, nennt man die Dezibel über S9 als Zusatz.

Beispiel:   Welcher Empfangsspannung entspricht die Angabe S9+40 dB auf Kurzwelle?

Lösung : S9 = 50 µV. 40 dB entsprechen dem Spannungsfaktor 100.   50 µV · 100 = 5000 µV = 5 mV

ehemalige Prüfungsfrage

TF403   Um wie viel S-Stufen müsste die S-Meter-Anzeige Ihres Empfängers steigen, wenn Ihr Partner die Sendeleistung von 10 Watt auf 40 Watt erhöht? Um ...
	eine S-Stufe
	zwei S-Stufen
	vier S-Stufen
	acht S-Stufen

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TF404   Ein Funkamateur kommt laut S-Meter mit S7 an. Dann schaltet er seine Endstufe ein und bittet um einen erneuten Rapport. Das S-Meter zeigt S9+8dB. Um welchen Faktor müsste der Funkamateur seine Leistung erhöht haben?
	120-fach
	20-fach
	10-fach
	100-fach

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TF405   Ein Funkamateur hat eine Endstufe, welche die Leistung verzehnfacht (von 10 auf 100 Watt). Ohne seine Endstufe zeigt Ihr S-Meter genau S8. Auf welchen Wert müsste die Anzeige Ihres S-Meters ansteigen, wenn er die Endstufe dazuschaltet?
	S9+4 dB
	S18
	S10+10 dB
	S9+9 dB

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TF406   Wie groß ist der Unterschied von S4 nach S7 in dB?
	3 dB
	9 dB
	18 dB
	24 dB

Lösungsweg (hier klicken zum Anzeigen):

Pegel

Häufig werden Leistungs- oder Spannungsangaben auf einen festgelegten Wert bezogen. Dann lassen sich Aussagen über die tatsächliche Leistung machen. Der Pegel in der Hochfrequenztechnik entspricht dem Pegel, den man von den Wasserstandsangaben kennt. Man kann den Wasserstand zum Beispiel an einer Stelle angeben als 6,15 m. Man kann aber auch sagen, dass heute der Pegel 15 cm höher als normal ist (6,00 m).

In der übertragungstechnik gibt es verschiedene Normal- oder Nullwerte, auf die man sich bezieht, Watt (dBW), Milliwatt (dBm), Pikowatt (dBpW), Volt (dBV), Mikrovolt (dBµV). Hier im Lehrgang Klasse E werden nur Leistungspegel besprochen.

In der NF- und in der HF-Technik werden die Pegel dBm und dBW verwendet. Es bedeutet, dass der Bezugswert 1 Milliwatt bzw. 1 Watt beträgt. Bei sehr kleinen Leistungen in der HF-Messtechnik und bei Angaben über Störleistungen (EMV) wird der Bezugswert 1 Pikowatt verwendet, deshalb pW hinter dB. Die Formeln für den Leistungspegel lauten

\[ p = 10 \cdot \lg \left( \frac{P}{1 \ \text{mW}} \right) \text{dBm} \] \[ p = 10 \cdot \lg \left( \frac{P}{1 \ \text{pW}} \right) \text{dBpW} \]

ehemalige Prüfungsfrage

TH304   Welcher der nachfolgenden Zusammenhänge ist richtig?
	0 dBm entspricht 1 mW; 3 dBm entspricht 1,4 mW; 20 dBm entspricht 10 mW
	0 dBm entspricht 0 mW; 3 dBm entspricht 30 mW; 20 dBm entspricht 200 mW
	1 dBm entspricht 0 mW; 2 dBm entspricht 3 mW; 100 dBm entspricht 20 mW
	0 dBm entspricht 1 mW; 3 dBm entspricht 2 mW; 20 dBm entspricht 100 mW

Lösungsweg (hier klicken zum Anzeigen):

Die Pegelwerte lassen sich mit Angaben in dB-Gewinn und solchen in dB-Dämpfung verrechnen. Ist beispielsweise der Pegel an einer Stelle 15 dBm und man hat man dahinter einen Verstärker mit 10 dB Gewinn, ist hinter dem Verstärker der Pegel 25 dBm. Folgt dann noch ein Kabel mit 2 dB Dämpfung, beträgt der Pegel am Ende des Kabels 23 dBm.

Oder umgekehrt: Hat man beispielsweise vor der Senderendstufe einen Pegel von 30 dBm und ist danach der Pegel 36 dBm, hat die Senderendstufe eine Verstärkung von 6 dB (nicht dBm!).

Merke: dB gilt immer für Verhältnisse,
dBm ist immer ein absoluter Wert.

Hochfrequenzleitungen

Hochfrequenzleitungen dienen dazu, entweder die vom Sender produzierte HF-Energie zur Antenne zu übertragen oder umgekehrt, die von der Antenne aufgefangene HF-Energie zum Empfänger zu leiten. In der Sendertechnik soll die Hochfrequenzleistung möglichst vollständig zur Antenne gelangen. Deshalb müssen verlustarme Leitungen verwendet werden. Es gibt zwei Arten von HF-Leitungen: Die Paralleldraht- oder Flachbandleitung und das Koaxialkabel (Bild 10-4).

Wellenwiderstand

Eine Leitung besteht im Prinzip aus der Reihenschaltung vieler kleiner Spulen und der Parallelschaltung vieler kleiner Kondensatoren (Bild 10-5 A). Berücksichtigt man noch den Leitungswiderstand R’ und den Isolationswiderstand R_P, erhält man das exakte Leitungsersatzbild (Bild 10-5 B).

Man nennt die Kapazität pro Meter Länge  einer  Leitung  den   Kapazitätsbelag C’

und die Induktivität pro Meter den Induktivitätsbelag L’. Aus diesen beiden Werten kann man den wichtigsten Kennwert einer Leitung berechnen, den Wellenwiderstand.

\[ Z_\mathcal{W} = \sqrt{\frac{L'}{C'}} \]

Beispiel: Von einem Meter Kabel wurde im Leerlauf die Kapazität von C’=90 pF und bei Kurzschluss die Induktivität von L’=0,5 µH gemessen. Wie groß ist der Wellenwiderstand dieser Leitung?

Lösung: \[Z_\mathcal{W} = \sqrt{\frac{L'}{C'}} = \sqrt{\frac{0,5 \ \mu \text{H}}{90 \ \text{pF}}} = \sqrt{5555} \ \text{Ω} = \mathbf{74{,}5 \ Ω} \]

Der Wellenwiderstand ist unabhängig von der Länge der Leitung, denn verdoppelt man die Länge, erhält man doppelte Induktivität und doppelte Kapazität. Der Wellenwiderstand bleibt gleich. Er ist auch unabhängig von der Frequenz .

Der Wellenwiderstand ist der wichtigste Kennwert einer Hochfrequenzleitung. Sowohl die Antenne mit ihrem Fußpunktwiderstand wie auch der Sender mit seinem Ausgangswiderstand sollten normalerweise mit dem dazwischen geschalteten Wellenwiderstand des Kabels übereinstimmen. Andernfalls gibt es Fehlanpassungen, die sich durch so genannte stehende Wellen äußern und zu Fehlverhalten führen.

Anders ausgedrückt: Schließt man an das Ende einer Hochfrequenzleitung einen Widerstand an, der genau dem Wert des Wellenwiderstandes entspricht, wird alle Leistung an diesen Widerstand abgegeben. Man spricht dann von Leistungsanpassung . Es treten keine Reflexionen und damit keine stehenden Wellen auf.

Deshalb definiert man

Der Wellenwiderstand entspricht dem Abschlusswiderstand einer Leitung, bei dem keine stehenden Wellen auftreten.

Umgekehrt gilt: Treten stehende Wellen auf, ist der am Kabelanfang zu messende Widerstand nicht gleich dem Wellenwiderstand. Die Wellenwiderstände Z_w der Hochfrequenzleitungen sind vom Aufbau und vom Material abhängig. In der Praxis findet man folgende Werte:

Paralleldrahtleitungen:   Z_w = 150 Ω bis 600 Ω
Koaxialleitungen:   Z_w =  50 Ω bis 95 Ω

Für die Einspeisung unabgestimmter symmetrischer Antennen eignet sich die Paralleldrahtleitung (im Amateurfunk „Hühnerleiter“ genannt) wegen ihrer geringen Verluste hervorragend als Speiseleitung. Man kann sie fertig im Amateurfunk-Zubehörhandel kaufen oder auch selbst anfertigen, indem man zwei Antennendrähte mit Isolierspreizern auf einen Abstand von zirka 6 bis 10 cm bringt.

ehemalige Prüfungsfrage

TH307   Der Wellenwiderstand einer Leitung
	ist völlig frequenzunabhängig.
	hängt von der Beschaltung am Leitungsende ab.
	hängt von der Leitungslänge und der Beschaltung am Leitungsende ab.
	ist im HF-Bereich in etwa konstant und unabhängig vom Leitungsabschluss.

Kommentar : Völlig unabhängig gibt es nicht. Bei sehr sehr hohen Frequenzen ist der Wellenwiderstand auch von der Frequenz abhängig. Aber im normalen Frequenzbereich für Funkamateure ist der Wellenwiderstand konstant und wird durch den Aufbau der Leitung bestimmt.

ehemalige Prüfungsfrage

TH308   Koaxialkabel weisen typischerweise Wellenwiderstände von
	50, 300 und 600 Ohm auf.
	60, 120 und 240 Ohm auf.
	50, 60 und 75 Ohm auf.
	50, 75 und 240 Ohm auf.

ehemalige Prüfungsfrage

TH309   Welche Vorteile hat eine Paralleldraht-Speiseleitung gegenüber der Speisung über ein Koaxialkabel?
	Sie vermeidet Mantelwellen durch Wegfall der Abschirmung.
	Sie erlaubt leichtere Kontrolle des Wellenwiderstandes durch Verschieben der Spreizer.
	Sie bietet guten Blitzschutz durch niederohmige Drähte.
	Sie hat geringere Dämpfung und hohe Spannungsfestigkeit.

ehemalige Prüfungsfrage

TH311   Welche Leitungen sollten für die HF-Verbindungen zwischen Amateurfunk-Einrichtungen verwendet werden, um unerwünschte Abstrahlungen zu vermeiden?
	Hochwertige abgeschirmte Netzanschlusskabel
	Hochwertige Koaxialkabel
	Symmetrische Feederleitungen
	Unabgestimmte Speiseleitungen

Die Dämpfungsberechnung

Der zweite, wichtige Kennwert einer Hochfrequenzleitung ist die Dämpfung. Dämpfung bedeutet, dass nur noch ein Teil der Eingangshochfrequenzleistung am Ende der Leitung ankommt. Natürlich will man die Dämpfung in der übertragungstechnik gering halten.

Die Dämpfung hängt vom Verlustwiderstand der Leitung ab. Das ist primär der Leitungswiderstand der inneren Kupferleitung und des Geflechtes bei Koaxialkabeln. Je dicker der Innenleiter ist, desto geringer sind die Verluste. Desto dicker muss aber auch der Außenleiter sein. Diese Kabel sind teurer als dünne Leitungen.

Ferner hängen die Verluste vom Isolierstoff (Dielektrikum) ab. Am wenigsten Verluste haben Leitungen ohne Kunststofffüllung, also Luft als Dielektrikum. Diese Leitungen sind bei gleichem Innenleiter viel dicker. Sie sind aufwendiger in der Herstellung und dadurch teurer.

Die Dämpfung wird meist in Dezibel pro hundert Meter Länge bei einer bestimmten Frequenz angegeben. Verwendet man ein Kabel mit halber Länge, hat man auch nur die Hälfte der Dämpfung. Beim Aufbau der Antenne sollte man also darauf achten, dass der Weg vom Sender bis zur Antenne möglichst kurz wird.

Die Dämpfung ist außerdem frequenzabhängig. Im Fragenkatalog der BNetzA finden Sie ein Diagramm mit der Grunddämpfung gebräuchlicher Koaxialleitungen in Abhängigkeit von der Betriebsfrequenz. Dieses Diagramm erhalten Sie bei der Prüfung zusammen mit der Formelsammlung.

Ableseübung
Gegeben ist das Diagramm aus dem Fragenkatalog der BNetzA (siehe Anhang 4 in diesem Buch). Lesen Sie ab: Wie groß ist die Dämpfung je eines 100 m langen Kabelstücks vom Typ Aircell 7 bei den Frequenzen 29, 145, 435 und 1296 MHz?

Vergleichen Sie die abgelesenen Werte mit denen weiter unten in der Tabelle 10-1.

Vergleichen Sie einmal die Dämpfung von RG58 mit dem nicht viel dickeren Aircell 7 bei 145 MHz. RG58 hat eine fast dreimal so hohe Dämpfung, ist also nur für sehr kurze Verbindungsstücke, nicht aber als Antennenzuleitung geeignet. Verwechseln Sie in der Praxis RG58 nicht mit RG59 (75 Ohm!).

Typ	Außen-ø	Zw	Dämpfung in dB auf 100 m bei
			3,5 MHz	29 MHz	145 MHz	435 MHz	1296 MHz
RG 58	5,8 mm	50 Ω	2,9	9	20	33	64
RG 59	6,3 mm	75 Ω	-	-	-	-	-
RG213 U	10,3 mm	50 Ω	0,6	2,2	5,8	11	22
RG213 (MIL)	10,3 mm	50 Ω	1,2	3,7	8,7	14	28
Aircell 7	7,3 mm	50 Ω	0,8	2,9	7,5	13	28
Aircom Plus	10,8 mm	50 Ω	0,48	1,7	4,2	7,6	15

Tabelle 10-1: Wellenwiderstand und Dämpfung gebräuchlicher Standard-Koaxkabel

ehemalige Prüfungsfrage

TH306   Welche Dämpfung hat ein 20 m langes Koaxkabel vom Typ RG58 bei 29 MHz? (siehe hierzu Diagramm ...)
	4,5 dB
	1,8 dB
	9,0 dB
	1,2 dB

Kommentar : Beachten Sie, dass die Angaben der Dämpfung im Dämpfungsdiagramm aus der Formelsammlung auf 100 m bezogen sind. Bei 20 m Länge ist die abgelesene Dämpfung durch fünf zu teilen.

ehemalige Prüfungsfrage

TH305   Welche Dämpfung hat ein 25 m langes Koaxkabel vom Typ Aircell 7 bei 145 MHz? (siehe hierzu Diagramm)
	1,9 dB
	7,5 dB
	3,75 dB
	1,5 dB

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TH301   Am Ende einer Leitung ist nur noch ein Viertel der Leistung vorhanden. Wie groß ist das Dämpfungsmaß des Kabels?
	3 dB
	6 dB
	10 dB
	16 dB

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TH302   Am Ende einer Leitung ist nur noch ein Zehntel der Leistung vorhanden. Wie groß ist das Dämpfungsmaß des Kabels?
	16 dB
	3 dB
	6 dB
	10 dB

Lösungsweg (hier klicken zum Anzeigen):

Die Anpassung

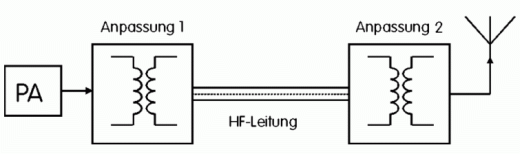
Anpassung in der Hochfrequenztechnik bedeutet, dass auf der einen Seite der Arbeits- oder Außenwiderstand des Senders mit der angeschlossenen HF-Leitung und auf der anderen Seite die Antennenimpedanz mit dem Wellenwiderstand des Kabels übereinstimmt.

Die Transistoren oder Röhren einer Senderendstufe (PA, power amplifier) müssen bei eingangsseitig voller Aussteuerung und ge­gebener Betriebsspannung einen bestimmten Lastwiderstand R_L vorfinden, wenn sie die maximal mögliche Ausgangsleistung abgeben sollen. Die Größenordnung des optimalen R_L liegt bei wenigen Ohm bei Transistoren und bis zu einigen Kiloohm bei Röhren.

Mittels Anpassgliedern wird der jeweilige Lastwiderstand R_L in den heute üblichen Senderausgangswiderstand R_a von 50 Ohm transformiert. Wird nun an den 50-Ω-Ausgang ein Koaxialkabel mit einem Wellenwiderstand von 50 Ω angeschlossen, das seinerseits mit einer Antenne verbunden ist, deren Eingangswiderstand bei 50 Ω liegt, gibt der Sender die maximal mögliche Leistung ab.

Weicht jedoch die Antennenimpedanz wesentlich von 50 Ω ab, etwa wegen zu geringer Aufbauhöhe oder weil man sich mit dem Transceiver wesentlich von der Resonanzfrequenz der Antenne entfernt hat, findet die PA eine abweichende Impedanz vor und die Leistungsabgabe sinkt.

Das Stehwellenverhältnis SWR, VSWR

Wie gut eine Antenne an die Zuleitung oder die Zuleitung an den Senderausgang angepasst ist, kann man mit dem Stehwellenverhältnis (SWR standing wave ratio oder VSWR voltage standing wave ratio) beschreiben.

Schickt man hochfrequente Leistung auf ein Kabel und wird wegen einer Fehlanpassung der Antenne an das Kabel nicht alle Energie abgenommen, wird dieser Teil reflektiert und wandert wieder zurück in Richtung Sender. Dabei überlagert sich diese rücklaufende Welle u_r mit der hinlaufenden Welle u_h (Bild 10-8). Dadurch entstehen in regelmäßigen Abständen Wellenberge (Summe aus hinlaufender und rücklaufender Welle) und Wellentäler (Differenz aus hinlaufender und rücklaufender Welle). Diese an bestimmten Stellen auftretenden Maxima U_max und Minima U_min bezeichnet man als stehende Wellen und das Verhältnis davon als Stehwellenverhältnis SWR standing wave ratio.

\[ SWR = \frac{U_{max}}{U_{min}} = \frac{u_h + u_r}{u_h - u_r} \]

Mehr zu SWR-Berechnungen und der praktischen Messtechnik dazu finden Sie im Buch im Kapitel 17: Messtechnik. Nur eines schon vorweg: Ein SWR von 1 (oder 1 zu 1 ) bedeutet vollkommene Anpassung.

Die Symmetrierung

Außer der eigentlichen Widerstandsanpassung muss bei Speisung von symmetrischen Antennen mit unsymmetrischen Kabeln auch noch symmetriert werden. Symmetrische Antennen sind alle Arten von Dipolen, unsymmetrische Antennen sind solche, die gegen Erde erregt werden (zum Beispiel λ/4-Vertikalstrahler). Symmetrische Kabel sind Paralleldrahtleitungen, unsymmetrische Kabel sind Koaxialkabel.

Wird eine symmetrische Antenne direkt an ein Koaxialkabel angeschlossen, so entstehen durch die Unsymmetrie Ausgleichsströme auf dem Mantel des Kabels, so genannte Mantelwellen . Damit strahlt ein solches Kabel HF-Energie ab, was bei benachbarten Zuleitungskabeln für Rundfunk- und Fernsehgeräte zu unerwünschten störenden Beeinflussungen führen kann. Zudem steigen die Verluste und das Strahlungsdiagramm der Antenne wird verzerrt.

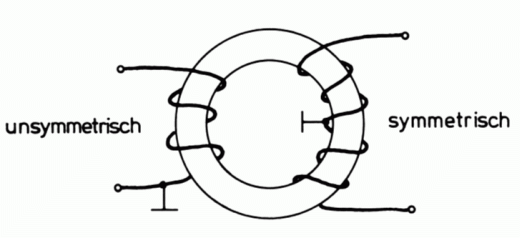
Zur Symmetrierung wird ein Breitbandsymmetrierübertrager (Balun genannt) verwendet. Balun kommt aus dem Englischen von balanced (symmetrisch) - unbalanced (unsymmetrisch), wie er im Bild 10-9 zu sehen ist. Es kann auch eine Mantelwellendrossel eingesetzt werden (siehe Prüfungsfrage TH405).

ehemalige Prüfungsfrage

TH403   Welche Auswirkungen hat es, wenn eine symmetrische Antenne (Dipol) mit einem Koaxkabel gleicher Impedanz gespeist wird?
	Es treten keine nennenswerten Auswirkungen auf, da die Antenne angepasst ist und die Speisung über ein Koaxkabel erfolgt, dessen Außenleiter Erdpotenzial hat.
	Die Richtcharakteristik der Antenne wird verformt und es können Mantelwellen auftreten.
	Am Speisepunkt der Antenne treten gegenphasige Spannungen und Ströme gleicher Größe auf, die eine Fehlanpassung hervorrufen.
	Es treten Polarisationsdrehungen auf, die von der Kabellänge abhängig sind.

ehemalige Prüfungsfrage

TH310   Wann ist eine Speiseleitung unsymmetrisch? Sie ist unsymmetrisch, wenn ...
	die hin- und zurücklaufende Leistung verschieden sind.
	sie außerhalb ihrer Resonanzfrequenz betrieben wird.
	die beiden Leiter unterschiedlich geformt sind, z.B. Koaxialkabel.
	die Koaxial-Leitung Spannung gegen Erde führt.

ehemalige Prüfungsfrage

TH404   Ein symmetrischer Halbwellendipol wird direkt über ein Koaxialkabel von einem Sender gespeist. Das Kabel ist senkrecht am Haus entlang verlegt und verursacht geringe Störungen. Um das Problem weiter zu verringern, empfiehlt es sich ...
	das Koaxialkabel durch eine Eindrahtspeiseleitung zu ersetzen.
	beim Koaxialkabel alle 5 m eine Schleife mit 3 Windungen einzulegen.
	das Koaxialkabel in einem Kunststoffrohr zur mechanischen Schirmung unterzubringen.
	den Dipol über ein Symmetrierglied zu speisen.

ehemalige Prüfungsfrage

TH405   Auf einem Ferritkern sind etliche Windungen Koaxial-kabel aufgewickelt. Diese Anordnung kann dazu dienen, ...
	statische Aufladungen zu verhindern.
	eine Antennenleitung abzustimmen.
	Mantelwellen zu dämpfen.
	Oberwellen zu unterdrücken.

Stecker und Adapter

Die Kabel werden an ihren Enden nicht in den Geräten angelötet, sondern mit Steckern versehen, die an die Gerätebuchsen angeschraubt werden. Für Kurzwelle und auch noch gelegentlich im 2-m-Band verwendet man das UHF-System, meistens PL-Stecker und PL-Buchse genannt. Für das 70-cm-Band und auch für das 2-m-Band verwendet man das N-System und für Messgerätekabel, für Handfunkgeräte und für Sender kleiner Leistung (etwa bis 20 Watt) das BNC-System. Für VHF/UHF-Handfunkgeräte verwendet man heutzutage die sehr kleinen SMA-Stecker.

Stecker- system	Verwendung
UHF	Kurzwelle, auch 2-Meter-Band
N	70-cm-Band, 2-m-Band
BNC	Messgeräte, Handfunkgeräte Sender bis 20 W
SMA	VHF-/UHF- Handfunkgeräte

ehemalige Prüfungsfrage

TH312   Welches der folgenden Koaxsteckverbindersysteme ist für sehr hohe Frequenzen (70-cm-Band) und hohe Leistungen am besten geeignet?
	N
	SMA
	UHF
	BNC

Viel Erfolg beim Lehrgang wünscht Ihnen Eckart Moltrecht DJ4UF!

Nach Oben

Zur Lehrgangs-Übersicht

Copyright-Hinweis:
	Dieser DARC-Online-Lehrgang wurde mit freundlicher Genehmigung des Autors Eckart K. W. Moltrecht aus seinen Büchern "Amateurfunk-Lehrgang für das Amateurfunkzeugnis" aus dem VTH-Verlag (möglicherweise einer älteren Auflage!) für das Internet umgewandelt. Das Copyright liegt beim Autor und beim Verlag. Mehr über den Autor!
	Die Darstellung auch nur von Auszügen oder Zeichnungen oder Fotos im Internet ist untersagt. Für die private Verwendung können Sie gern eine Genehmigung beim Autor erhalten. Schreiben Sie eine E-Mail an eckart.moltrecht(at)gmail.com!

Letzte Bearbeitung: 23.05.2017 DJ4UF, 04.04.2020 DH8GHH
Fehlermeldungen mit Linkangabe an DH8GHH@darc.de