In diesem Kapitel geht um grundsätzliche Begriffe aus den Grundlagen der Elektrotechnik.

Inhaltsübersicht

• Die elektrische Spannung
• Die Spannungsmessung
• Der elektrische Strom
• Die Stromstärke
• Die Ladungsmenge
• Wechselstrom, Wechselspannung
• Die Frequenz
• Die Periodendauer
• Der Effektivwert der Wechselspannung

Die elektrische Spannung

Sie wissen sicher, dass in einem Atom gleich viel negative Ladungen (Elektronen) und positive Ladungen (Protonen) vorhanden sind. Nach außen ist ein Atom und damit das gesamte Material, das aus diesen Atomen besteht, elektrisch neutral.

Gelingt es irgendwie, dieses natürliche Gleichgewicht zwischen den positiven und den negativen Ladungen aufzuheben (zu stören), so werden die voneinander getrennten verschiedenen Ladungen das Bestreben haben, durch die Anziehungskräfte wieder zusammen zu kommen.

Das Ausgleichsbestreben unterschiedlicher elektrischer Ladungen nennt man elektrische Spannung.

Das Trennen der Ladungen bei einer Spannungsquelle geschieht durch Energiezufuhr, zum Beispiel Reibung (Glasstab), chemische Vorgänge (Batterie, Akkumulator), durch Bewegen eines Magneten in einer Drahtschleife (Induktion beim Generator), durch Wärmewirkung (Thermoelement), durch Belichtung (Fotoelement), durch Druck (Piezoeffekt beim Feuerzeug) und so weiter.

Die Elektrode (Anschlussklemme) einer Spannungsquelle, an welcher Elektronenüberschuss herrscht, ist der Minuspol, denn die negative Ladung der Elektronen überwiegt. Am Pluspol einer Spannungsquelle herrscht Elektronenmangel.

Alle Bauelemente in der Elektrotechnik stellt man zeichnerisch durch ein (genormtes) Schaltzeichen dar. Eine Gleichspannungsquelle (Monozelle) wird durch folgendes Zeichen dargestellt.

Das Formelzeichen für die elektrische Spannung ist U (merke: Unterschied). Die Einheit für die Spannung ist das Volt, abgekürzt V.

Beispiele
• Die Netzspannung im Haushalt beträgt U = 230 V.
• Die Spannung eines Akkumulators im Auto beträgt U = 12 V.

Neben dieser Grundeinheit 1 Volt verwendet man Vielfache und Teile dieser Einheit. Wie es beispielsweise beim Meter Millimeter und Kilometer gibt, verwendet man in der Elektrotechnik Kilovolt, Millivolt oder Mikrovolt.

1 kV  = 10³V  = 1 000 V
1 mV = 10^-3V = 0,001 V
1 µV  = 10^-6V = 0,000001V

Es gibt sehr hohe und sehr niedrige Spannungen. Im Amateurfunk verarbeitet ein guter Empfänger Signale, die mit einer Spannung von weniger als ein Mikrovolt (1 µV = ein Millionstel Volt) von der Antenne geliefert werden, zu brauchbaren Lautstärken. In Sendern arbeiten starke Endstufen manchmal mit Röhren, die mit Spannungen von mehr als zwei Kilovolt betrieben werden.

Die Spannungsmessung

Die Spannung kann mit einem Spannungsmesser zwischen zwei Punkten einer Schaltung gemessen werden, zwischen denen ein Potenzialunterschied herrscht. Der Spannungsmesser muss parallel zur zu messenden Spannung geschaltet werden.

Ein Spannungsmesser wird rund gezeichnet (Anzeigegerät). Er erhält als Zusatzsymbol ein V für die Einheit Volt im Schaltzeichen (Bild 2-2). Er wird immer zur zu messenden Spannung parallel geschaltet.

Beim Anschluss eines Spannungsmessers ist auf die Polarität zu achten, das heißt: Der Pluspol des Spannungsmessers wird an die Plusklemme der Batterie und der Minuspol an die Minusklemme angeschlossen. Es gibt elektronische Messgeräte (digitale Messgeräte), die eine automatische Umschaltung vornehmen. Die Polarität wird hierbei durch ein Plus- oder Minuszeichen angezeigt. Siehe auch Kapitel E17: Messtechnik!

Alle Spannungen über 50 V sind lebensgefährlich. Ein Berühren kann tödlich sein.

Deshalb darf bei Spannungen über 42 Volt nach den Vorschriften des Verbandes Deutscher Elektrotechniker (VDE) das zufällige Berühren Spannung führender Teile nicht möglich sein. Bei Spannungen über 50 Volt sind besondere Schutzmaßnahmen erforderlich, in Kapitel E18 beschrieben werden.

Die Reihenschaltung von Spannungsquellen

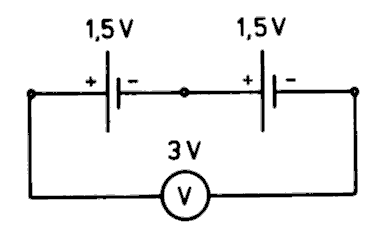
Mehrere Spannungsquellen, zum Beispiel handelsübliche 1,5-V-Zellen, lassen sich zu so genannten Batterien zusammenschalten. Bild 2-3 zeigt: Schaltet man zum Beispiel zwei Zellen von je 1,5 Volt so hintereinander, dass der Pluspol der einen mit dem Minuspol der anderen zusammengeschaltet wird, misst man mit einem Spannungsmesser eine Gesamtspannung von 3 Volt.

Man nennt diese Schaltung eine Reihenschaltung oder Serienschaltung von Spannungsquellen.

Merken Sie sich: In einer Reihenschaltung addieren sich die Teilspannungen zur Gesamtspannung.

Haben Sie einen Spannungsmesser? Als Funkamateur sollten Sie ein Vielfachmessgerät besitzen, denn Sie werden immer wieder in die Verlegenheit kommen, eine Spannung oder einen Strom messen zu wollen.

Messen Sie einmal die Gesamtspannung folgender Gegenreihenschaltung (Bild 2-4), bei der die Monozellen so hintereinander geschaltet sind, dass sich die beiden Pluspole oder die beiden Minuspole berühren.

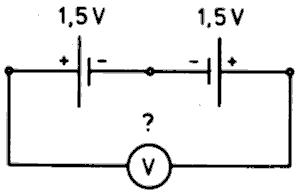
Bei der Gegenreihenschaltung werden die beiden Spannungen voneinander subtrahiert (abgezogen). Bei der Schaltung im Bild 2-4 messen Sie bei genau gleichen Teilspannungen eine Gesamtspannung von null Volt.

Testen Sie sich selbst, indem Sie auf den entsprechenden Button klicken, aber nur einmal in jeder Aufgabe!

ehemalige Prüfungsfrage

TB201  Welche Spannung zeigt der Spannungsmesser in folgender Schaltung?
	3 V
	0 V
	-3 V
	1,5 V

Steht bei Ihnen nun nur einmal das Wort "Richtig" und keinmal das Wort "Falsch"? Gut.

Es lassen sich beliebig viele Einzelzellen zu einer hohen Gesamtspannung zusammenschalten. Beim Bleiakkumulator, wie er im Auto verwendet wird, werden zum Beispiel 6 Zellen von je 2 Volt so hintereinander geschaltet, dass die Gesamtspannung 12 Volt beträgt.

Der elektrische Strom

Elektrische Spannung entsteht durch Ladungstrennung. Verbindet man nach der Trennung die beiden Pole einer Spannungsquelle mit einem elektrischen Leiter, findet ein Ladungsausgleich statt. Den Ladungsausgleich beziehungsweise Ladungstransport nennt man elektrischen Strom.

Die Bewegung von Ladungsträgern allein ist noch kein elektrischer Strom, denn die Elektronen bewegen sich unter dem Einfluss der Temperatur ständig regellos umher. Erst wenn die Bewegung der Ladungsträger im Mittel in einer Richtung verläuft, findet ein Ladungstransport statt. In diesem Fall spricht man von elektrischem Strom.

Für die Stromrichtung wurde früher die Richtung vom Pluspol zum Minuspol festgelegt. Man nennt diese Definition der Stromrichtung „technische Stromrichtung“. Erst später fand man heraus, dass sich in Wirklichkeit die Ladungsträger in umgekehrter Richtung bewegen. In Kapitel 13 wird noch näher darauf eingegangen.

ehemalige Prüfungsfrage

TB203  Was versteht man unter „technischer Stromrichtung“ in der Elektrotechnik?
	Man nimmt an, dass der Strom vom Pluspol zum Minuspol fließt.
	Man nimmt an, dass der Strom vom Minuspol zum Pluspol fließt.
	Es ist die Flussrichtung der Elektronen vom Minuspol zum Pluspol.
	Es ist die Flussrichtung der Elektronen vom Pluspol zum Minuspol.

Merke: Elektrischer Strom ist die gerichtete Bewegung von Ladungsträgern.

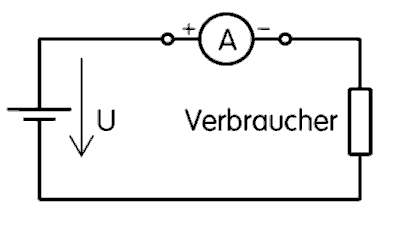
Ein elektrischer Strom kann nur fließen, wenn eine Spannungsquelle vorhanden ist, an die ein geschlossener Stromkreis angeschlossen ist. Ein geschlossener Stromkreis besteht aus der Spannungsquelle, dem so genannten Verbraucher (hier Glühlampe) und den Verbindungsleitungen (Bild 2-6).

ehemalige Prüfungsfrage

TB204  Kann in folgender Schaltung von zwei gleichen Spannungsquellen Strom fließen?
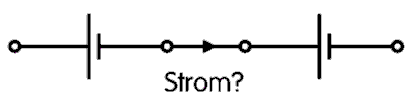Welche Begründung ist richtig?
	Nein, weil der Pluspol mit dem Minuspol verbunden ist.
	Ja, sogar Kurzschlussstrom, weil der Pluspol mit dem Minuspol  verbunden ist.
	Nein, weil kein geschlossener Stromkreis vorhanden ist.
	Ja. Der Strom hängt vom Innenwiderstand der Batterien ab.

Kommentar: Nein, denn es ist kein geschlossener Stromkreis vorhanden. Es handelt sich hier nur um die Reihenschaltung von zwei Spannungsquellen.

Die Stromstärke

Um über den elektrischen Strom eine Aussage machen zu können, muss man ihn mit geeigneten Anzeigegeräten messen. Dazu benötigt man eine Einheit der Stromstärke.

Merke: Das Formelzeichen für die elektrische Stromstärke ist I (Intensität).
Die Einheit der elektrischen Stromstärke ist das Ampere, Abkürzung A.

In der Nachrichtentechnik verwendet man häufig Teile der Einheit von 1 Ampere.

1 Milliampere = 1 mA = 10^-3A = 1/ 1000 A
1 Mikroampere = 1 µA = 10^-6A = 1/ 1000000 A

Die Stromstärke wird gemessen, indem man einen Strommesser (Amperemeter) in den geschlossenen Stromkreis einschleift. Dazu muss eine Verbindungsleitung aufgetrennt und der Strommesser „in Reihe“ geschaltet werden (Bild 2-8). Mehr zur Strom- und Spannungsmessung finden Sie im Kapitel E17: Messtechnik!

Die Ladungsmenge

Beim Strom handelt es sich um die Bewegung von elektrischen Ladungsträgern. Wenn der Strom eine Zeitlang geflossen ist, hat man eine bestimmte Ladungsmenge transportiert. Es gilt der Zusammenhang

Ladungsmenge Q ist Stromstärke I mal Zeit t, als Formel geschrieben

\[ Q = I \cdot t \]

Die Einheit der Ladungsmenge ergibt sich aus dieser Formel als abgeleitete Einheit Ampere mal Sekunden oder Ampere mal Sekunden oder kurz Amperesekunde, abgekürzt As.

Für diese Einheit Amperesekunde hat man eine neue Einheit definiert. Man hat sie Coulomb genannt und mit C abgekürzt.

1 C = 1 A · 1 s = 1 As

Aufgabe: Schreiben Sie folgende Tabelle ab und tragen Sie zur übung die Formelbuchstaben und die Abkürzungen der Einheiten ein. Anschließend können Sie durch Klicken auf das entsprechende Feld Ihre Lösung prüfen.

Größe	Formel- zeichen	Einheit
Ladungsmenge
Spannung
Strom

Eine Amperesekunde ist eine ziemlich kleine Einheit. In der Praxis rechnet man mit Amperestunden. Es gilt:

1 Stunde = 60 Minuten = 3 600 Sekunden

1 h = 60 min = 3 600 s

Beispiel: Ein Akku wird 10 Stunden lang mit einer Stromstärke von 5,5 Ampere geladen. Wie groß ist die aufgenommene Ladungsmenge in Amperestunden?

Lösung: Q = I · t = 5,5 A · 10 h = 55 Ah

Der Akku hat eine Ladungsmenge von 55 Amperestunden aufgenommen.

ehemalige Prüfungsfrage

TB205  Wie lange könnte man mit einem voll geladenen Akku mit 55 Ah einen Amateurfunk-Empfänger betreiben, der einen Strom von 0,8 Ampere aufnimmt?
	68 Stunden und 75 Minuten
	Genau 44 Stunden
	6 Stunden 52 min und 30 s
	68 Stunden und 45 Minuten

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TB202  Folgende Schaltung eines Akkus besteht aus Zellen von je 2 V. Jede Zelle kann 10 Ah Ladung liefern. Welche Daten hat der Akku?
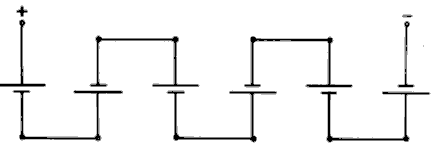	12 V / 60 Ah
	12 V / 10 Ah
	2 V / 10 Ah
	2 V / 60 Ah

Lösungsweg (hier klicken zum Anzeigen):

Wechselstrom, Wechselspannung

Bisher wurde in diesem Lehrgang eine gleich bleibende Bewegungsrichtung der Ladungsträger angenommen. Dies nennt man Gleichstrom. Ändert sich die Bewegungsrichtung der Ladungsträger ständig, fließt also der Strom hin und her, spricht man von Wechselstrombeziehungsweise als Ursache des Stromes von Wechselspannung.

Fließt beispielsweise eine Zeitlang der Strom gleichmäßig in eine Richtung – sagen wir: Plusrichtung – und danach eine Zeitlang in Minusrichtung, also umgekehrt, kann man diese Tatsache grafisch in Form eines Diagramms darstellen. Man zeichnet eine horizontale Linie. Diese stellt die Zeit dar. Man schreibt ein t (time) an die Achse. Nach oben und unten wird der Strom aufgetragen. Dabei bedeutet nach oben die Plusrichtung und nach unten die Minusrichtung. Bild 2-9 A stellt dann den eben beschriebenen Wechselstrom dar. Man nennt diese Kurvenform nach ihrem Aussehen „rechteckförmig“.

In der Praxis sieht der technische Wechselstrom aus der Netzsteckdose anders aus. Er entspricht der Kurvenform im Bild 2-9 B. Man nennt diese Form „sinusförmig“. Eine solche Wechselspannung, bei der sich die Kurvenform regelmäßig wiederholt, heißt periodische Wechselspannung. Die Periode ist die Zeit, bis sich der Vorgang wiederholt.

Nicht-sinusförmige Signale werden erst im Lehrgang Klasse A Kapitel 13 behandelt. Deshalb können Sie die Prüfungsfrage TB702 mit dem Wissen aus diesem Lehrgang Klasse E nicht beantworten. Bisher ist diese Prüfungsfrage wohl auch noch nicht auf einem der Prüfungsfragenblätter aufgetaucht. Streichen Sie diese Frage einfach!

Die Frequenz

Die Anzahl der Perioden je Sekunde ist die Frequenz f einer Wechselspannung mit der Einheit Hertz (Hz).

1 Hertz = 1 Periode je Sekunde

\[ 1 \ \text{Hz} = \frac{1}{\text{s}} \]

Die Anzahl der Perioden ist nur eine Zahl ohne Einheit. Deshalb steht im Zähler nur eine Eins.

Das Stromnetz in Europa hat 50 Perioden pro Sekunde, also 50 Hertz. In den USA beträgt die Frequenz 60 Hertz. Tonfrequenz zur Übertragung von Sprache oder Musik zum Beispiel enthält die Frequenzen 20 Hz bis 20 kHz. Der Frequenzbereich zur übertragung von Sprache beträgt im Amateurfunk 300 Hz bis 3 kHz. Hochfrequenz ist der Bereich zur Funkübertragung. Er enthält den Frequenzbereich von zirka 100 kHz bei Langwelle bis weit in den Gigahertzbereich hinein für Satellitenfunk.

Maßeinheit	Abkürzung	Zehnerpotenz	Angabe in Hz	Umrechnung
1 Kilohertz	1 kHz	103Hz	1 000 Hz
1 Megahertz	1 MHz	106Hz	1 000 000 Hz	1 000 kHz
1 Gigahertz	1 GHz	109Hz	1 000 000 000 Hz	1 000 MHz

ehemalige Prüfungsfrage

TB606  Welche Bezeichnung ist für eine Schwingung von 145 000 000 Perioden pro Sekunde richtig?
	145 kHz
	145 MHz
	145 Kilometer
	145 km/s

Die Periodendauer

Die Zeitdauer T für eine vollständige Schwingung (1 Periode, siehe Bild 2-10) nennt man Periodendauer. Sie beträgt zum Beispiel für den technischen Wechselstrom eine fünfzigstel Sekunde.

\[ \frac{1}{50} \text{s} = 0{,}02 \ \text{s} = 20 \ \text{ms} \]

Allgemein kann mit folgender Formel die Periodendauer aus der Frequenz errechnet werden.

\[ T = \frac{1}{f} \]

wobei auch hier die Einheiten in ihrer Grundform Sekunde und Hertz eingesetzt werden.

Umgekehrt ist

\[ f = \frac{1}{T} \]

ehemalige Prüfungsfrage

TB607  Die Periodendauer von 50 µs entspricht einer Frequenz von
	200 kHz
	2 MHz
	20 kHz
	20 MHz

Üblicherweise benutzt man diese Formel, um aus einer Periodendauer die Frequenz zu ermitteln, denn auf dem Bildschirm eines Oszilloskops kann man die Periodendauer ganz gut ablesen. In dem Diagramm der folgenden Aufgabe ist horizontal die Zeit im Maßstab
3 µs pro Zeiteinheit (Kästchen, Division) aufgetragen.
Um die Aufgabe zu lösen, müssen Sie die Periodendauer bestimmen, indem Sie die Anzahl der Kästchen für eine volle Periode zählen und diese Anzahl mit der Zeiteinheit pro Kästchen multiplizieren.

ehemalige Prüfungsfrage

TB610  Welche Frequenz hat die in diesem Oszillogramm dargestellte Spannung?
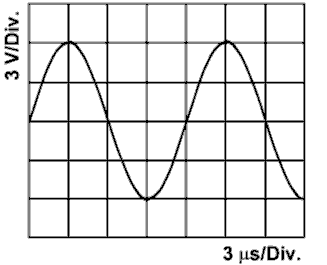	83,3 kHz
	833,3 kHz
	8,3 MHz
	83,3 MHz

Lösungsweg (hier klicken zum Anzeigen):

ehemalige Prüfungsfrage

TB611  Welche Frequenz hat das in diesem Schirmbild dargestellte Signal?
	8,33 kHz
	16,7 MHz
	8,33 MHz
	833 kHz

Kommentar: Der Lösungsweg ist der gleiche wie bei TB610. Nur sind es diesmal 0,03 µs pro Teilung anstatt 3 µs, also Faktor 100. Hundertfach kleinere Periodendauer bedeutet hundertfach höhere Frequenz. Aber rechnen Sie selbst!

Der Effektivwert der Wechselspannung

Stellen Sie sich folgenden Versuch vor: Sie legen eine Glühlampe an eine bestimmte Gleichspannung. Anschließend wiederholen Sie den Vorgang mit einer Wechselspannung, die Sie so lange verändern, bis die Glühlampe genau so hell leuchtet wie zuvor mit der Gleichspannung. Betrachten Sie nun die eingestellten Werte wieder in einem Diagramm, so stellen Sie fest, dass der höchste Wert der Wechselspannung höher liegt als die Gleichspannung. Genauer gesagt liegt die Gleichspannung bei ca. 70% des Maximalwerts der Wechselspannung. Diesen Wert nennt man Effektivwert der Wechselspannung U_eff. Da der Effektivwert einer gleich großen Gleichspannung entspricht, schreibt man dafür häufig auch nur den Großbuchstaben U.

Beispiel:
Die Netzwechselspannung im Haushalt beträgt U = 230 Volt.

Bei einem sinusförmigen Verlauf der Wechselspannung kann man einen einfachen Zusammenhang zwischen dem Maximalwert (Scheitelwert oder Spitzenwert) U_max , dem Spitze-Spitze-Wert U_ss und dem Effektivwert U_eff nachweisen. Der Spitze-Spitze-Wert ist das Doppelte vom Spitzenwert (Bild 2-11).

Wenn der Scheitelwert einer sinusförmigen Wechselspannung bekannt ist, kann man den Effektivwert mit folgender Formel berechnen. Eine mathematische Ableitung müssen wir uns hier ersparen.

\[ \boxed{U_{ \textit{eff}} = \frac{U_{max}}{\sqrt{2}}} \]

Prüfen Sie mal mit dem Taschenrechner:

\[ \sqrt{2} = 1{,}414 \]

und der Kehrwert davon

\[ \frac{1}{\sqrt{2}} = \frac{1}{1{,}414} = 0{,}707 \]

Also kann man auch rechnen

\[ \boxed{U_{\textit{eff}} = 0{,}707 \cdot U_{max}} \]

Der Effektivwert einer sinusförmigen Wechselspannung beträgt etwa 70,7 % des Scheitelwertes. Gleiches gilt auch für den Strom. In der Praxis rechnet man häufig einfach mit 0,7 oder 70 Prozent.

ehemalige Prüfungsfrage

TB612  Eine sinusförmige Wechselspannung hat einen Spitzenwert von 12 Volt. Wie groß ist der Effektivwert der Wechselspannung?
	6 V
	8,5 V
	17 V
	24 V

Lösungsweg (hier klicken zum Anzeigen):

Allgemein gilt: Wird bei einer Wechselspannung oder bei einem Wechselstrom keine nähere Angabe gemacht, ist grundsätzlich der Effektivwert gemeint.

Bei Messungen mit dem Oszilloskop kann man den Wert von der positiven Spitze bis unten zur negativen Spitze leichter ablesen. Man nennt ihn Spitze-Spitze-Wert. Aus Bild 2-11 geht hervor, wie er mit dem Spitzenwert oder dem Effektivwert zusammenhängt. Der Spitze-Spitze-Wert ist also doppelt so groß wie der Spitzenwert.

ehemalige Prüfungsfrage

TB613  Ein sinusförmiges Signal hat einen Effektivwert von 12 V. Wie groß ist der Spitze-Spitze-Wert?
	36,4 V
	24 V
	16,97 V
	33,9 V

Lösungsweg (hier klicken zum Anzeigen):

Viel Erfolg beim Lehrgang wünscht Ihnen Eckart Moltrecht DJ4UF!

Nach Oben

Zur Lehrgangs-Übersicht

Copyright-Hinweis:
	Dieser DARC-Online-Lehrgang wurde mit freundlicher Genehmigung des Autors Eckart K. W. Moltrecht aus seinen Büchern "Amateurfunk-Lehrgang für das Amateurfunkzeugnis" aus dem VTH-Verlag (möglicherweise einer älteren Auflage!) für das Internet umgewandelt. Das Copyright liegt beim Autor und beim Verlag. Mehr über den Autor!
	Die Darstellung auch nur von Auszügen oder Zeichnungen oder Fotos im Internet ist untersagt. Für die private Verwendung können Sie gern eine Genehmigung beim Autor erhalten. Schreiben Sie eine E-Mail an eckart.moltrecht(at)gmail.com!

Letzte Bearbeitung: 24.05.2017 DJ4UF, 04.04.2020 DH8GHH
Fehlermeldungen mit Linkangabe an DH8GHH@darc.de