Neue Ausbildungsplattform 50ohm.de
Das Ausbildungsmaterial für den neuen Fragenkatalog (2024) findest du auf www.50Ohm.de
Hinweis: Der Lehrgang auf dieser Seite bezieht sich auf die alten Fragenkataloge, nach denen nur noch bis April 2024 geprüft wurde.
Kapitel 7: Schwingkreis, Filter
Inhaltsübersicht
- Der Schwingungsvorgang
- Die Resonanzfrequenz
- Die Reihenschwingkreis
- Die Parallelschwingkreis
- Die Bandbreite
- Tiefpass, Hochpass
Eine sehr wichtige Schaltung in der Hochfrequenztechnik und damit in der Amateurfunktechnik ist der Schwingkreis als ein Sonderfall der Zusammenschaltung von Spule und Kondensator. Man unterscheidet den Serienschwingkreis als Reihenschaltung und den Parallelschwingkreis als Parallelschaltung von Spule und Kondensator wie sie in folgendem Bild 7-1 dargestellt sind.

Der Schwingungsvorgang
Den beiden Bauelementen Spule und Kondensator ist gemeinsam, dass sie während einer bestimmten Zeit Energie aufnehmen und speichern können, die sie dann später wieder abzugeben vermögen.
Der Kondensator benötigt elektrische Energie zum Aufbau des elektrischen Feldes (Laden des Kondensators), die dann bei der Entladung wieder frei wird. Die Spule benötigt ebenfalls elektrische Energie, aber zum Aufbau eines magnetischen Feldes. Beim Abbau dieses Feldes wird diese Energie wieder frei. Dies zeigt sich zum Beispiel beim Abschalten von Spulen in elektrischen Schaltkreisen, wo die frei werdende Energie eine hohe Spannung am Ausschaltkontakt bewirkt.
Gibt man auf einen dieser zusammen geschalteten Bauelemente Energie, zum Beispiel durch eine von außen her zugeführte Ladung des Kondensators, so pendelt die Energie zwischen beiden hin und her. Spule und Kondensator wirken abwechselnd als Energiequelle und als Energiespeicher. Siehe Bild 7-2 auf der nächsten Seite!
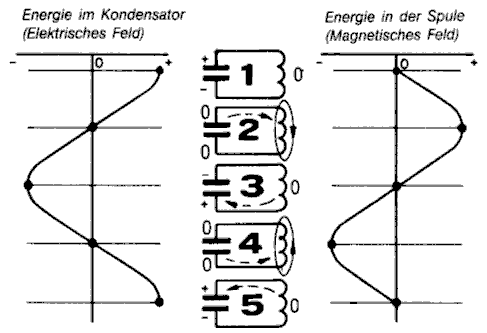
Schließt man (gedanklich) einen geladenen Kondensator an eine Spule an (siehe Bild 2, Fall 1), so wird sich der Kondensator über die Spule entladen, wodurch in der Spule durch den Stromfluss ein magnetisches Feld entsteht, während das elektrische Feld im Kondensator abgebaut wird.
Nach Beendigung der Entladung steckt die gesamte Energie in Form des Magnetfeldes in der Spule. Sobald kein Strom mehr fließt (Fall 2), bricht das Magnetfeld zusammen und die dadurch erzeugte Induktionsspannung bewirkt einen Strom, mit dem der Kondensator in entgegen gesetzter Richtung wieder geladen wird.
Wenn der Schwingkreis keine Verluste hätte, würde nun die gesamte Energie wieder im Kondensator stecken (Fall 3) und nun der Vorgang wieder in umgekehrter Richtung ablaufen (Fall 4 und Fall 5). Es ergäbe sich eine ungedämpfte Schwingung (Bild 7-3).

Da aber jede Spule einen Ohmschen Widerstand (Kupferdraht!) besitzt, wird bei diesem Pendelvorgang jedes Mal ein wenig Energie in Wärme umgesetzt, so dass die Schwingungen immer kleiner werden. Man sagt, die Schwingungen sind gedämpft. Wenn man ungedämpfte Schwingungen erzeugen will (Sender, Oszillator), muss dem Schwingkreis von außen die entsprechende Energie im richtigen Augenblick wieder zugeführt werden.
Die Resonanzfrequenz
Die Zeitdauer einer Pendelschwingung hängt von den Größen der Kapazität und der Induktivität ab. Ist die Kapazität zum Beispiel sehr groß, dauert es sehr lange bis der Kondensator entladen ist. Die Frequenz der Schwingung ist also sehr niedrig. Die Frequenz, die sich nach einmaligem Anstoßen einstellt, nennt man Resonanzfrequenz.
Aus der Kapazität und der Induktivität eines Schwingkreises kann man die Resonanzfrequenz nach folgender Formel berechnen.
\[ f_{res} = \frac{1}{2 \cdot \pi \cdot \sqrt{L \cdot C}} \]Diese Formel – nach dem Ohmschen Gesetz die zweitwichtigste Formel für den Funkamateur – wird als "Thomsonsche Schwingkreisformel" bezeichnet. Aus der Formel kann man erkennen, dass die Resonanzfrequenz fres umgekehrt proportional zur Wurzel aus Induktivität L und Kapazität C ist.
ehemalige Prüfungsfrage
| TD204 Wie ändert sich die Resonanzfrequenz eines Schwingkreises, wenn 1. die Spule weniger Windungen erhält, 2. die Länge der Spule durch Zusammenschieben der Drahtwicklung verringert wird, 3. ein Ferritkern in das Innere der Spule gebracht wird? | |
|---|---|
| Die Resonanzfrequenz wird bei 1. und 2. kleiner und bei 3. größer. | |
| Die Resonanzfrequenz wird bei 1. kleiner und bei 2. und 3. größer. | |
| Die Resonanzfrequenz wird bei 1. und 2. größer und bei 3. kleiner. | |
| Die Resonanzfrequenz wird bei 1. größer und bei 2. und 3. kleiner. | |
Lösungsweg (hier klicken zum Anzeigen):
Reihenschwingkreis
Schaltet man die Bauelemente Spule und Kondensator hintereinander (in Reihe also), so nennt man diese Schaltung Reihenschwingkreis (Bild 7-4).

Experiment
Wenn Sie im Rahmen eines Amateurfunklehrgangs die Möglichkeit haben, mit Schul- oder Clubgeräten zu arbeiten, führen Sie einmal folgenden Versuch durch. Bauen Sie die Schaltung nach Bild 7-4 mit L = 100 mH und C = 10 nF auf. Schalten Sie einen Strommesser für Wechselstrom mit möglichst niedrigem Innenwiderstand in Reihe. Ändern Sie dann die Frequenz zwischen zirka 100 Hertz und 10 Kilohertz und messen Sie den Strom. Achten Sie darauf, dass sich die Generatorspannung möglichst nicht ändert.
Für diejenigen, die keine Messmöglichkeit haben, sei folgende Tabelle mit Messwerten vorgegeben. Hinweis: Der gemessene Strom kann bei Ihrer Messung kleiner oder größer sein. Es hängt vom Widerstand der Spule und vom Innenwiderstand des Generators ab.
Bei konstanter Generatorspannung von 2,5 V wurden gemessen:
| f | 1 | 2 | 3 | 4 | 4,7 | 5 | 5,3 | 6 | 7 | 10 | kHz |
| I | 3 | 5 | 8 | 16 | 70 | 100 | 70 | 20 | 12 | 5 | mA |
| Z | 125 | Ω |
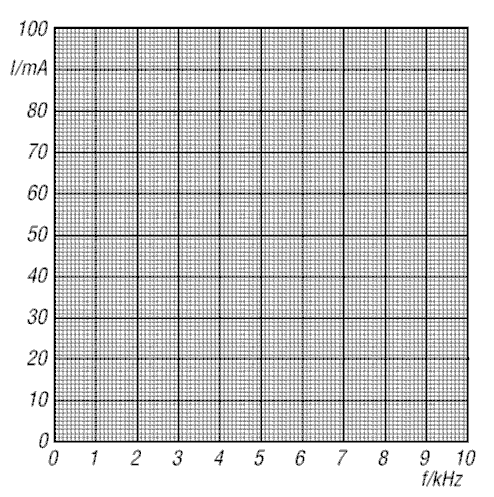

Aufgabe: Tragen Sie zunächst die Messwerte für den Strom in das Diagramm Bild 7-5 links ein.
Wenn man bei Wechselstromwerten die anliegende Spannung durch den fließenden Strom teilt, erhält man wie beim Ohmschen Gesetz einen Widerstandswert in Ohm, den man hier aber Scheinwiderstand Z nennt. Bei 6 kHz wurden bei U = 2,5 V beispielsweise 20 mA gemessen. Dies ergibt einen Scheinwiderstand von
\[ Z = \frac{U}{I} = \frac{2,5 \ \text{V}}{0,02 \ \text{A}} = 125 \ \text{Ω} \]Aufgabe: Berechnen Sie mit Ihren gemessenen Werten oder mit den Werten aus obiger Tabelle den Scheinwiderstand bei den angegebenen Frequenzen. Tragen Sie die Ergebnisse in die Tabelle und anschließend auch in das rechte Diagramm von Bild 7-5 ein.
Wenn Sie richtig gerechnet und gezeichnet haben, ergeben sich Kurven, die bei f = 5 kHz ein Strommaximum beziehungsweise ein Scheinwiderstandsminimum haben.
Solche Kurven, also die Abhängigkeit des Stromes, der Spannung oder des Scheinwiderstandes von der Frequenz eines Schwingkreises, nennt man Impedanzkurven. Den Scheinwiderstand bei der Resonanzfrequenz nennt man Resonanzwiderstand. Er ist beim Reihenschwingkreis recht klein. Hier beträgt er beispielsweise 25 Ohm. Siehe folgende Prüfungsfrage TD201!
ehemalige Prüfungsfrage
| TD201 Der Impedanzfrequenzgang in der Abbildung zeigt die Kennlinie | |
|---|---|
 | |
| eines Parallelschwingkreises. | |
| eines Serienschwingkreises. | |
| einer Induktivität. | |
| einer Kapazität. | |
Diese im Niederfrequenzbereich durchgeführten überlegungen gelten ebenso im Hochfrequenzbereich. Allerdings treten hier außer den Ohmschen Verlusten (Wicklungswiderstand der Spule) auch noch Verluste im Kernmaterial und Verluste der verminderten Leitfähigkeit des Drahtes infolge des „Skineffektes“ auf. Skineffekt bedeutet: Bei hohen Frequenzen fließt der Strom nicht mehr gleichmäßig verteilt durch den Querschnitt, sondern mehr an der Oberfläche (Skin) des Drahtes.
Merken Sie sich:
Bei einem Reihenschwingkreis ist der Resonanzwiderstand klein. Er ist ungefähr so groß wie der Verlustwiderstand der Spule.
Ein Reihenschwingkreis wird wegen der Eigenschaft, dass er bei einer Frequenz (Resonanzfrequenz) praktisch einen Kurzschluss darstellt, zur Störungsunterdrückung beim gestörten Empfänger eingesetzt (Saugkreis). Im folgenden Bild 7-6 ist eine typische Anwendung des Serienschwingkreises im Amateurfunk dargestellt.

Einen Saugkreis finden Sie in Prüfungsfrage TD209! Diese Prüfungsaufgabe können Sie allerdings erst beantworten, wenn Sie auch die folgenden Kapitel über Hochpass und Tiefpass durchgearbeitet haben. Also: Noch Geduld!
Parallelschwingkreis
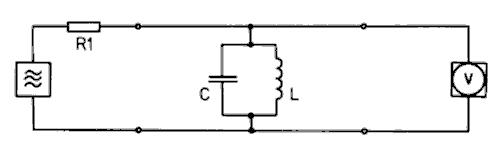
Der Schwingkreis ist für einen Funkamateur sehr wichtig. Deshalb machen wir wieder einen Laborversuch. Sie benötigen dazu einen Frequenzgenerator und ein Oszilloskop oder ein Wechselspannungsmessgerät für den Frequenzbereich bis 10 Kilohertz. Ferner benötigen Sie für den Schwingkreis die Bauelemente aus dem Versuch vom Reihenschwingkreis.
Experiment
Schalten Sie die beiden Bauelemente L = 100 mH und C = 10 nF, die Sie beim Reihenschwingkreis verwendet haben, nach Schaltung Bild 7-7 parallel. Um den Strom einigermaßen konstant zu halten, vergrößern Sie den Innenwiderstand des Generators durch Hinzufügen eines Widerstandes auf 1 MΩ. Wählen Sie eine Generatorspannung von zirka 3 Volt. Messen Sie die Spannung am Schwingkreis mit einem Oszilloskop und tragen Sie die Messwerte in Abhängigkeit von der Frequenz in eine ähnliche wie die folgende Tabelle ein.
Ergeben sich bei Ihnen ähnliche Messwerte wie die in folgender Tabelle?
| f | 1 | 2 | 3 | 4 | 4,7 | 5 | 5,3 | 6 | 7 | 10 | kHz |
| U | 0,02 | 0,04 | 0,06 | 0,1 | 0,7 | 1 | 0,7 | 0,15 | 0,1 | 0,05 | V |
| Z | 20 | 333 | kΩ |
Den Strom kann man als ungefähr konstant annehmen mit 3V / 1 MΩ = 3 µA.
Aufgabe: Tragen Sie die Messwerte für die Spannung und die berechneten Werte für den Scheinwiderstand in die Diagramme Bild 7-8 ein.
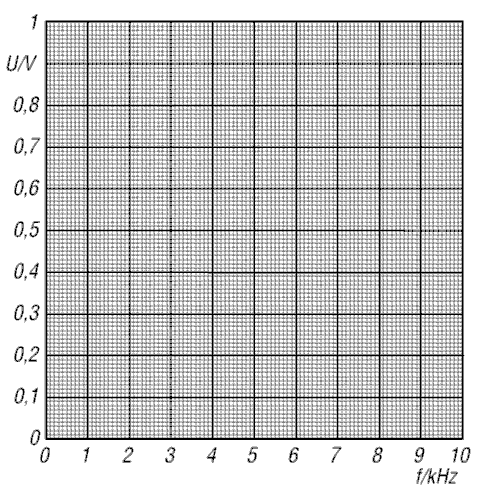

Aufgabe zu Bild 7-8: Berechnen Sie für die einzelnen gemessenen Spannungen den jeweiligen Scheinwiderstand und tragen Sie die Werte in obige Tabelle ein. Zwei Werte sind bereits eingetragen.
Es sollten sich Kurven wie beim Reihenschwingkreis ergeben, allerdings in beiden Fällen ein Maximum.
Merke: Bei einem Parallelschwingkreis ist der Scheinwiderstand bei der Resonanzfrequenz am größten.
Bei dieser Frequenz erreicht auch die Spannung ihr Maximum, wenn man den Schwingkreis mit einem Generator mit hohem Innenwiderstand speist. Wegen dieser Eigenschaft wird der Parallelschwingkreis in Hochfrequenzverstärkern (siehe Amateurfunk-Lehrgang für die Klasse A, Lektion 7) eingesetzt.
Die zu verstärkende Spannung erreicht bei der Resonanzfrequenz ihren Höchstwert. Eine Anwendung ist der Sperrkreis . Schaltet man einen Parallelschwingkreis in Reihe zum Eingang eines Empfängers, wird die Frequenz um die Resonanzfrequenz herum (Bandbreite: Siehe folgender Abschnitt) gesperrt , weil der Parallelschwingkreis ja einen sehr großen Widerstand für diesen Frequenzbereich darstellt.
Zusammenfassung: Beim Parallelschwingkreis ist der Scheinwiderstand bei der Resonanzfrequenz am größten. Beim Reihenschwingkreis ist er dort am kleinsten (Bild 7-9).
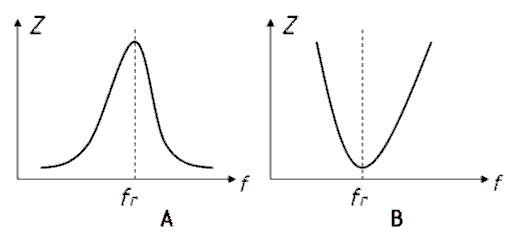
fr im Bild 7-9 steht für „Resonanzfrequenz“. Zur Erinnerung: Das ist die Eigenfrequenz eines Schwingkreises.
ehemalige Prüfungsfrage
| TD202 Der im folgenden Bild dargestellte Impedanzfrequenzgang ist typisch für | |
|---|---|
 | |
| einen Kondensator. | |
| eine Spule. | |
| einen Parallelschwingkreis. | |
| einen Serienschwingkreis. | |
ehemalige Prüfungsfrage
| TD203 Welcher Scheinwiderstand passt zu dem neben der jeweiligen Schaltung dargestellten Verlauf des Scheinwiderstandes? | |
|---|---|
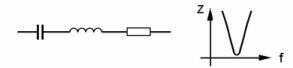 | |
 | |
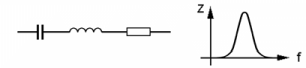 | |
 | |
ehemalige Prüfungsfrage
| TD205 Wie verhält sich ein Parallelschwingkreis bei der Resonanzfrequenz? | |
|---|---|
| Wie ein hochohmiger Widerstand. | |
| Wie ein niederohmiger Widerstand. | |
| Wie ein Kondensator mit sehr kleiner Kapazität. | |
| Wie eine Spule mit sehr großer Induktivität. | |
Bandbreite
Ein Hochfrequenzverstärker, der mit einem Schwingkreis als Arbeitswiderstand beschaltet ist, verstärkt nicht nur eine einzige Frequenz, sondern einen gewissen Frequenzbereich, ein Frequenzband. Diesen bevorzugten Bereich, bei der die Spannung oder der Scheinwiderstand jeweils auf 70 Prozent des Maximalwertes abgefallen ist, nennt man Bandbreite (Bild 7-10). Mehr darüber im Lehrgang für die Klasse A!

Tiefpass, Hochpass
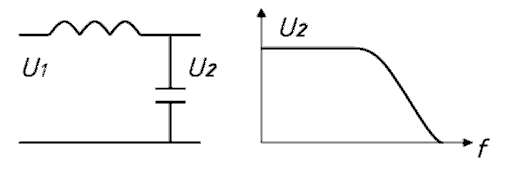
Durch eine weitere Zusammenschaltung von Spule und Kondensator ergeben sich Schaltungen, die man Tiefpass oder Hochpass nennt. Schaltet man eine Spule in Reihe zum Signalweg und den Kondensator dahinter parallel zum Signal, erhält man einen Tiefpass (Bild 7-11). Die Tiefpasswirkung lässt folgendermaßen beschreiben.
Hat man eine zunächst niedrige Frequenz, stellt die Spule einen geringen induktiven Widerstand dar und der Kondensator hat einen großen kapazitiven Widerstand. Es entsteht ein Spannungsteiler, bei dem ein kleiner Widerstand oben in Serie und ein großer am Ausgang parallel geschaltet sind. Nur wenig Spannung geht verloren. Die Ausgangsspannung U2 ist fast genau so groß wie die Eingangsspannung U1 (siehe Bild 7-11 rechts).
Steigt die Frequenz, wird der induktive Widerstand größer und der kapazitive kleiner. Immer mehr Spannung geht verloren. Die hohen Frequenzen kommen also nicht so gut durch oder anders herum ausgedrückt: Die tiefen Frequenzen werden gut durchgelassen (sie können „passieren“ – durch gehen) – Tiefpass. Die Frequenz, bei der die Ausgangsspannung nur noch 70 Prozent so groß ist wie die Eingangsspannung, nennt man Grenzfrequenz.
ehemalige Prüfungsfrage
| TD207 Was stellt die folgende Schaltung dar? | |
|---|---|
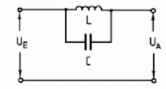 | |
| Saugkreis | |
| Bandpass | |
| Sperrkreis | |
| Tiefpass | |
ehemalige Prüfungsfrage
| TD209 Was stellt die folgende Schaltung dar? | |
|---|---|
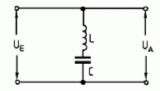 | |
| Sperrkreis | |
| Saugkreis | |
| Bandpass | |
| Tiefpass | |

In der Schaltung Bild 7-12 ist gegenüber Bild 7-11 der Kondensator mit der Spule vertauscht. Haben wir eine tiefe Frequenz, stellt der Kondensator in Serie einen großen Widerstand dar und die Spule einen geringen. Deshalb kommt wenig Spannung durch. Erst bei hohen Frequenzen lässt der Kondensator die Spannung "passieren" und die Spule schließt nicht mehr kurz: Hoch pass.
Diese Schaltungen werden im Amateurfunk recht häufig angewendet, um beispielsweise den Kurzwellenbereich zu sperren und den UKW- und Fernsehbereich durchzulassen, wenn durch Sender elektromagnetische Unverträglichkeiten beim Radio- oder Fernsehempfang auftreten.
Auch hier gilt: Viel ausführlicher wird dieses Kapitel „Tiefpass, Hochpass“ im Amateurfunklehrgang für die Klasse A behandelt.
ehemalige Prüfungsfrage
| TD206 Was stellt die folgende Schaltung dar? | |
|---|---|
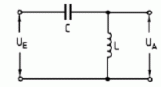 | |
| Sperrkreis | |
| Hochpass | |
| Bandpass | |
| Tiefpass | |
Merkhilfe: Kondensator oben: Hochpass
Kondensator unten: Tiefpass
ehemalige Prüfungsfrage
| TD208 Was stellt die folgende Schaltung dar? | |
|---|---|
 | |
| Tiefpass | |
| Sperrkreis | |
| Bandpass | |
| Hochpass | |
ehemalige Prüfungsfrage
| TD210 Welche der nachfolgenden Eigenschaften trifft auf einen Hochpass zu? | |
|---|---|
| Frequenzen unterhalb der Grenzfrequenz werden verstärkt. | |
| Frequenzen oberhalb der Grenzfrequenz werden stark bedämpft. | |
| Frequenzen oberhalb der Grenzfrequenz werden durchgelassen. | |
| Frequenzen unterhalb der Grenzfrequenz werden ungedämpft durchgelassen. | |
Viel Erfolg beim Lehrgang wünscht Ihnen Eckart Moltrecht DJ4UF!
| Copyright-Hinweis: | |
|---|---|
 | Dieser DARC-Online-Lehrgang wurde mit freundlicher Genehmigung des Autors Eckart K. W. Moltrecht aus seinen Büchern "Amateurfunk-Lehrgang für das Amateurfunkzeugnis" aus dem VTH-Verlag (möglicherweise einer älteren Auflage!) für das Internet umgewandelt. Das Copyright liegt beim Autor und beim Verlag. Mehr über den Autor! |
 | Die Darstellung auch nur von Auszügen oder Zeichnungen oder Fotos im Internet ist untersagt. Für die private Verwendung können Sie gern eine Genehmigung beim Autor erhalten. Schreiben Sie eine E-Mail an eckart.moltrecht(at)gmail.com! |
Letzte Bearbeitungen:
06.11.2016 DK2DQ, 24.07.2017 DJ4UF, 04.04.2020 DH8GHH
Fehlermeldungen, insbesondere, wenn Sie mit dem Smartphone arbeiten, mit Linkangabe bitte an DH8GHH@darc.de!

