Neue Ausbildungsplattform 50ohm.de
Das Ausbildungsmaterial für den neuen Fragenkatalog (2024) findest du auf www.50Ohm.de
Hinweis: Der Lehrgang auf dieser Seite bezieht sich auf die alten Fragenkataloge, nach denen nur noch bis April 2024 geprüft wurde.
Kapitel 8: Elektromagnetisches Feld
Inhaltsübersicht
Mit Hilfe der Funktechnik sollen Informationen drahtlos übertragen werden. Zum Aufbau einer solchen Funkstrecke wird auf der einen Seite ein Sender benötigt, der mit der zu übertragenden Nachricht moduliert wird, und auf der anderen Seite ein Empfänger, der die Nachricht verarbeiten kann.
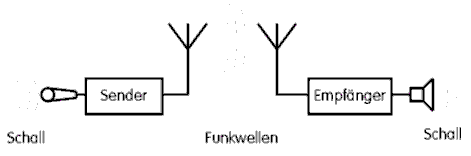
Durch die Erzeugung und die Ausbreitung elektromagnetischer Wellen ist es möglich, diese Nachricht über große Entfernungen drahtlos zu übertragen. Dies ist die eigentliche Funktechnik.
Diese elektromagnetischen Wellen bestehen aus elektrischen und magnetischen Feldern mit einer sehr hohen Frequenz (Hochfrequenz). In den folgenden Abschnitten soll nun der Versuch gemacht werden, diese unsichtbaren Felder ein wenig begreifbar zu machen.
Dazu wird zunächst gezeigt, wie statische (unveränderliche) elektrische und magnetische Felder erzeugt werden und wie man sie durch Linien darstellt. In Wirklichkeit sind es natürlich keine Linien, sondern Felder, die wie die Luft überall vorhanden sind, aber unterschiedliche Feldstärke haben.
Das elektrische Feld

Wird an zwei voneinander isolierten Metallplatten eine Gleichspannung gelegt, entsteht im Raum zwischen den Platten ein elektrisches Feld. Wenn die Platten parallel zueinander sind, entsteht ein gleichmäßiges (homogenes) Feld, das durch parallele Linien dargestellt wird (Bild 8-2).
Testen Sie sich, indem Sie links auf die Fragezeichen klicken, aber nur einmal in jeder Tabelle!
ehemalige Prüfungsfrage
| TB302 Wie nennt man das Feld zwischen zwei parallelen Kondensatorplatten bei Anschluss an Gleichspannung? | |
|---|---|
 | |
| Homogenes elektrisches Feld | |
| Homogenes magnetisches Feld | |
| Polarisiertes elektrisches Feld | |
| Polarisiertes magnetisches Feld | |
Sie haben die Frage gut beantwortet, wenn Sie in der linken Spalte nur einmal das Wort "Richtig" sehen und keinmal "Falsch".
Die Stärke des elektrischen Feldes ist umso größer, je höher die Spannung U zwischen den Platten und je kleiner der Abstand (d) ist. Die Formel lautet
$$\begin{aligned} E = \frac{U}{d} && \text{mit der Einheit} && \frac{\text{V}}{\text{m}} \end{aligned}$$ehemalige Prüfungsfrage
| TB301 Welche Einheit wird für die elektrische Feldstärke verwendet? | |
|---|---|
| Watt pro Quadratmeter (W/m2) | |
| Ampere pro Meter (A/m) | |
| Henry pro Meter (H/m) | |
| Volt pro Meter (V/m) | |
Magnetisches Feld

Wenn durch den Draht einer Zylinderspule wie in Bild 8-3 Gleichstrom fließt, entsteht im Innern ein gleichmäßiges magnetisches Feld. Eine Kompassnadel wird zum Beispiel dadurch bewegt. Dieses magnetische Feld wird beispielsweise bei Messgeräten zum Ausschlagen eines Zeigers, also zur Strommessung verwendet.
Die magnetische Feldstärke H zu berechnen, ist nicht ganz einfach. Deshalb wird hier keine Formel angegeben. Aber die Feldstärke H wird mit der Stromstärke I größer und mit der Länge der (geschlossenen) Feldlinie geringer. Die Einheit wird in Ampere pro Meter A/m angegeben.
ehemalige Prüfungsfrage
| TB401 Welche Einheit wird für die magnetische Feldstärke verwendet? | |
|---|---|
| Watt pro Quadratmeter (W/m2) | |
| Volt pro Meter (V/m) | |
| Ampere pro Meter (A/m) | |
| Henry pro Meter (H/m) | |
Ein einzelner Strom durchflossener Leiter erzeugt ein ringförmiges (konzentrisches) Magnetfeld. So sehen die magnetischen Feldlinien um einen Vertikalstrahler aus (Bild 8-4). Der Unterschied ist nur, dass sie sich in der Richtung und Stärke mit der Frequenz ändern.

ehemalige Prüfungsfrage
| TB402 Wie nennt man das Feld im Innern einer langen Zylinderspule beim Fließen eines Gleichstroms? | |
|---|---|
| Homogenes elektrisches Feld | |
| Zentriertes magnetisches Feld | |
| Konzentrisches Magnetfeld | |
| Homogenes magnetisches Feld | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB403 Wenn Strom durch einen gestreckten Leiter fließt, entsteht ein ... | |
|---|---|
| elektrisches Feld aus konzentrischen Kreisen um den Leiter. | |
| Magnetfeld aus konzentrischen Kreisen um den Leiter. | |
| homogenes Magnetfeld um den Leiter. | |
| homogenes elektrisches Feld um den Leiter. | |
Lösungsweg (hier klicken zum Anzeigen):
Magnetische Feldlinien können "verstärkt" werden, wenn man bestimmte Stoffe einfügt. Zu diesen Stoffen gehört insbesondere Eisen. Sie kennen dies sicher aus der Praxis, dass man mit einem Magneten Eisen gut anziehen kann. Man nennt solche Stoffe ferromagnetisch (ferrum = Eisen).
ehemalige Prüfungsfrage
| TB405 Welcher der nachfolgenden Werkstoffe ist ein ferromagnetischer Stoff? | |
|---|---|
| Chrom | |
| Kupfer | |
| Eisen | |
| Aluminium | |
Lösungsweg (hier klicken zum Anzeigen):
Elektromagnetisches Feld

Schaltet man nun einen Kondensator und eine Spule zu einem Schwingkreis zusammen und erzeugt man einen Wechselstrom in diesem Schwingkreis (zu Beispiel durch einen Sender), so entsteht im Kondensator ein wechselndes elektrisches Feld und in der Spule ein wechselndes Magnetfeld. Zusammen bilden sie ein elektromagnetisches Feld.
Werden die Kondensatorplatten dieses Schwingkreises auseinander gezogen, so verlaufen die elektrischen Feldlinien nicht nur innerhalb des Kondensators von einer Platte zur anderen, sondern sie gehen weit durch den Raum (Bild 8-5 a).
Zieht man auch noch die Spule auseinander, erhält man eine Dipolantenne (Bild 8-5 b). Die elektrischen Feldlinien verlaufen nun von der einen Seite des Drahtes zur anderen durch den Raum. Die magnetischen Feldlinien bilden geschlossene Kreise um den Draht.
Im Bild 8-5b erkennt man, dass die elektrischen Feldlinien weiter entfernt von der Antenne praktisch parallel zum Antennendraht und die magnetischen Feldlinien ringförmig (konzentrisch) um den Antennendraht verlaufen. Dies ist der typische Verlauf des elektromagnetischen Feldes um eine gestreckte Drahtantenne.
ehemalige Prüfungsfrage
| TB502 Wie erfolgt die Ausbreitung einer elektromagnetischen Welle? Die Ausbreitung erfolgt ... | |
|---|---|
| nur über das elektrische Feld. Das magnetische Feld ist nur im Nahfeld vorhanden. | |
| nur über das magnetische Feld. Das elektrische Feld ist nur im Nahfeld vorhanden. | |
| durch eine Wechselwirkung zwischen elektrischem und magnetischem Feld. | |
| Über die sich unabhängig voneinander ausbreitenden und senkrecht zueinander stehenden elektrischen und magnetischen Felder. | |
Polarisation

Anstatt eine Dipolantenne zu verwenden, kann man auch die Hälfte einer solchen Antenne gegen Erde erregen. Diese Marconi-Antenne steht dann senkrecht (vertikal). Auch die weiter hinten im Lehrgang behandelte Groundplane-Antenne (Kapitel 11) hat ein solches elektromagnetisches Feld.
Bei der Wellenausbreitung spricht man von horizontaler und vertikaler Polarisation. Hierbei wird die Richtung des elektrischen Feldes (E-Feld) als Bezug genommen. Wenn die Sendeantenne senkrecht auf dem Erdboden steht, verlaufen die elektrischen Feldlinien (X in Bild 8-6) von oben nach unten (vertikal) und die magnetischen Feldlinien (H-Feld) kreisförmig um die Sendeantenne herum parallel zum Erdboden (horizontal). Man spricht in diesem Fall von vertikaler Polarisation.
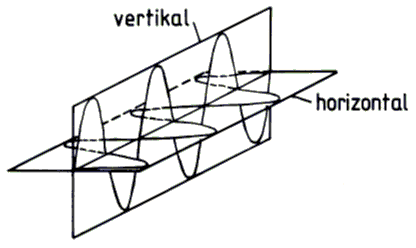
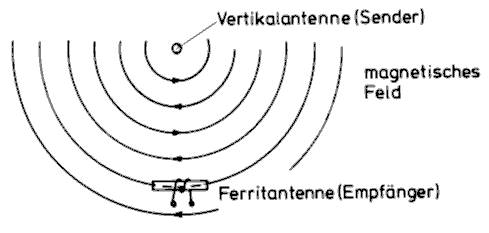
Die kreisförmigen Linien im Bild 8-8 sind die magnetischen Feldlinien und die von oben nach unten verlaufenden Feldlinien sind die elektrischen Feldlinien. Eine solche senkrecht nach oben zeigende Antenne heißt Vertikalantenne. Man sagt: Diese Antenne hat eine vertikale Polarisation.
Das magnetische Feld verläuft rechtwinklig (90°) zum elektrischen Feld, hier also waagerecht. Um die magnetischen Feldlinien zu empfangen, kann man eine Ferritantenne verwenden. Eine Ferritantenne ist ein zylindrisches Stück „Eisen“ (Ferritmaterial), auf das eine Spule gewickelt ist.
Eine Ferritantenne muss bei vertikaler Polarisation aber waagerecht angeordnet sein, so dass die horizontal verlaufenden magnetischen Feldlinien die Spule maximal durchsetzen, um die höchste Empfangsspannung zu liefern. Durch Drehung dieser Antenne kann man damit peilen. Wenn die Ferritantenne genau in Richtung Sendeantenne zeigt, gehen die Feldlinien quer durch den Ferritstab und nicht mehr durch das Innere der Spule und die Empfangsspannung ist gering. Solch eine Antenne wird bei Peilwettbewerben im Amateurfunk verwendet.
ehemalige Prüfungsfrage
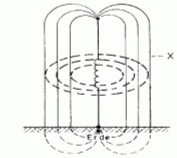
| TB303 Wie werden die mit X gekennzeichneten Feldlinien einer Vertikalantenne bezeichnet? | |
|---|---|
 | |
| Magnetische Feldlinien | |
| Elektrische Feldlinien | |
| Polarisierte Feldlinien | |
| Horizontale Feldlinien | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB404 Wie werden die mit X gekennzeichneten Feldlinien einer Vertikalantenne bezeichnet? | |
|---|---|
 | |
| Magnetische Feldlinien | |
| Elektrische Feldlinien | |
| Radiale Feldlinien | |
| Vertikale Feldlinien | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB501 Wodurch entsteht ein elektromagnetisches Feld?
Ein elektromagnetisches Feld entsteht, | |
|---|---|
| wenn ein zeitlich schnell veränderlicher Strom durch einen elektrischen Leiter fließt, dessen Länge mindestens 1/100 der Wellenlänge ist. | |
| wenn durch einen elektrischen Leiter, dessen Länge mindestens 1/100 der Wellenlänge ist, ein konstanter Strom fließt. | |
| wenn sich elektrische Ladungen in einem Leiter befinden, dessen Länge mindestens 1/100 der Wellenlänge ist. | |
| wenn an einem elektrischen Leiter, dessen Länge mindestens 1/100 der Wellenlänge ist, eine konstante Spannung angelegt wird. | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB503 Das folgende Bild zeigt die Feldlinien eines elektromagnetischen Feldes. Welche Polarisation hat die skizzierte Wellenfront? | |
|---|---|
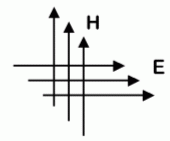 | |
| Vertikale Polarisation | |
| Rechtsdrehende Polarisation | |
| Horizontale Polarisation | |
| Zirkulare Polarisation | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB504 Der Winkel zwischen den elektrischen und magnetischen Feldkomponenten eines elektromagnetischen Feldes beträgt im Fernfeld | |
|---|---|
| 45°. | |
| 90°. | |
| 180°. | |
| 360°. | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB505 Die Polarisation des Sendesignals in der Hauptstrahlrichtung dieser Richtantenne ist | |
|---|---|
 | |
| vertikal. | |
| horizontal. | |
| rechtsdrehend. | |
| linksdrehend. | |
Lösungsweg (hier klicken zum Anzeigen):
Die Wellenlänge
Die elektromagnetischen Wellen breiten sich mit einer Geschwindigkeit wie der des Lichtes aus. Im Freien beträgt die Ausbreitungsgeschwindigkeit 300 000 km pro Sekunde. In Kabeln ist die Ausbreitungsgeschwindigkeit mit 200 000 bis 280 000 km pro Sekunde zwar etwas niedriger, aber immer noch unvorstellbar hoch. Um dennoch eine kleine Vorstellung zu geben: In einer Sekunde würden sich die elektromagnetischen Wellen mehr als siebenmal um die Erde bewegen beziehungsweise fast die Strecke Erde - Mond zurücklegen.
Wenn eine Welle eine Frequenz hätte von 1 Hertz (1 Schwingung pro Sekunde), wäre der Anfang dieser einen Welle bereits 300 000 km entfernt, wenn das Ende gerade abgestrahlt wird. Diese Entfernung bezeichnet man als Wellenlänge λ (gesprochen: lambda). Sie beträgt bei ein Hertz also 300 000 km im freien Raum. Nimmt man nun eine gegenüber 1 Hertz um eine Million höhere Frequenz, nämlich ein Megahertz, so ist der Anfang erst ein Millionstel so weit entfernt. Die Wellenlänge beträgt also 300 000 km geteilt durch eine Million, also 0,3 km oder 300 m.
Mathematisch betrachtet:
Für eine Million schreibt man in der Mathematik auch 106, das bedeutet eine 10, sechsmal mit sich selbst malgenommen oder eine 1 mit 6 Nullen. Damit
kann man dann einfacher mit dem Taschenrechner rechnen, indem man bei Exponent (EXP) einfach eine 6 eingibt. Für die Ausbreitungsgeschwindigkeit 300 000
Kilometer oder 300 000 000 m kann man auch schreiben
Bei 1 MHz beträgt die Wellenlänge also 300 m. Bei 10 MHz wären es dann 30 m oder bei 100 MHz noch 3 m.
Als Formel (Anhang 3!) schreibt man
\[ \begin{align} \lambda [\text{m}] &= \frac{c}{f[\text{Hz}]} \\ \\ \text{mit} \ c &= 3 \cdot 10^8 \frac{\text{m}}{\text{s}} \\ \\ \end{align} \]Allgemein gilt
\[ c = f \cdot \lambda \]Merke: Frequenz mal Wellenlänge ist konstant.
Diese Formel lässt sich, wie das ohmsche Gesetz, in Dreiecksform schreiben. Immer steht bei solch einem "Formeldreieck" das Produkt (also die mit Malzeichen verbundenen Größen) unten im Dreieck. Hier sind es f und λ.

So geht's:
Wenn f gesucht wird, hält man f zu und übrig bleiben c oberhalb und λ unterhalb vom Bruchstrich, also f gleich c geteilt durch lambda. Wenn λ
gesucht ist, hält man λ zu und übrig bleiben c oberhalb und f unterhalb des Bruchstrichs.
ehemalige Prüfungsfrage
| TB602 Welcher Wellenlänge λ entspricht die Frequenz 1,84 MHz? | |
|---|---|
| 16,3 m | |
| 163 m | |
| 0,613 m | |
| 61,3 m | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TI201 Die Ausbreitungsgeschwindigkeit freier elektromagnetischer Wellen beträgt etwa | |
|---|---|
| 3 000 000 km/s. | |
| 30 000 km/s. | |
| 300 000 km/s. | |
| 3 000 km/s. | |
Lösungshinweis (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB601 Welches ist die Einheit der Wellenlänge? | |
|---|---|
| m | |
| m/s | |
| Hz | |
| s/m | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB603 Welcher Wellenlänge λ entspricht die Frequenz 28,28 MHz? | |
|---|---|
| 163 m | |
| 9,49 m | |
| 10,6 m | |
| 61,3 m | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB604 Eine Wellenlänge von 2,06 m entspricht einer Frequenz von … | |
|---|---|
| 135,754 MHz | |
| 148,927 MHz | |
| 150,247 MHz | |
| 145,631 MHz | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB605 Eine Wellenlänge von 80,0 m entspricht einer Frequenz von … | |
|---|---|
| 3,75 MHz | |
| 3,65 MHz | |
| 3,56 MHz | |
| 3,57 MHz | |
Lösungsweg (hier klicken zum Anzeigen):
ehemalige Prüfungsfrage
| TB608 Den Frequenzbereich zwischen 30 und 300 MHz bezeichnet man als | |
|---|---|
| UHF (ultra high frequency) | |
| MF (medium frequency) | |
| VHF (very high frequency) | |
| SHF (super high frequency) | |
Lösungsweg (hier klicken zum Anzeigen):
| Band | Frequenzbereich |
|---|---|
| 160 m | 1,810 ... 2,000 MHz |
| 80 m | 3,500 ... 3,800 MHz |
| 40 m | 7,000 ... 7,200 MHz |
| 30 m | 10,100 ... 10,150 MHz |
| 20 m | 14,000 ... 14,350 MHz |
| 17 m | 18,068 ... 18,168 MHz |
| 15 m | 21,000 ... 21,450 MHz |
| 12 m | 24,890 ... 24,990 MHz |
| 10 m | 28,000 ... 29,700 MHz |
| 6 m | 50,080 ... 51,000 MHz |
| 2 m | 144 ... 146 MHz (VHF) |
| 70 cm | 430 ... 440 MHz (UHF) |
| 23 cm | 1240 ... 1300 MHz (SHF) |
| 3 cm | 10,0 ... 10,5 GHz |
Tabelle 8-1: der Amateurfunk-Frequenzbereiche (Hervorgehoben = Klasse E)
ehemalige Prüfungsfrage
| TB609 Das 70-cm-Band befindet sich im | |
|---|---|
| VHF-Bereich. | |
| UHF-Bereich. | |
| SHF-Bereich. | |
| EHF-Bereich. | |
Lösungshinweis (hier klicken zum Anzeigen):
Viel Erfolg beim Lehrgang wünscht Ihnen Eckart Moltrecht DJ4UF!
| Copyright-Hinweis: | |
|---|---|
 | Dieser DARC-Online-Lehrgang wurde mit freundlicher Genehmigung des Autors Eckart K. W. Moltrecht aus seinen Büchern "Amateurfunk-Lehrgang für das Amateurfunkzeugnis" aus dem VTH-Verlag (möglicherweise einer älteren Auflage!) für das Internet umgewandelt. Das Copyright liegt beim Autor und beim Verlag. Mehr über den Autor! |
 | Die Darstellung auch nur von Auszügen oder Zeichnungen oder Fotos im Internet ist untersagt. Für die private Verwendung können Sie gern eine Genehmigung beim Autor erhalten. Schreiben Sie eine E-Mail an eckart.moltrecht(at)gmail.com! |
Letzte Bearbeitungen: 24.07.2017 DJ4UF, 04.04.2020 DH8GHH
Fehlermeldungen mit Linkangabe an DH8GHH@darc.de

